This was a problem Harold Davenport gave me in 1963 and was to be chapter 1 of my PhD thesis. He was a fan of Hilbert's Irreducibility Theorem and recommended I study Karl Dörge's paper on that topic. (At one point in my paper, the use I made of that theorem is in fact unnecessary.) Many years later, R. Dvornicich and U. Zannier, On polynomials taking small values at integral arguments, Acta Arithmetica XLII (1982) 189-196, studied a generalization.
This used the 2x2 matrix point of view that R.F.C. Walters had successfully employed in his novel proofs of the continued fraction expansion of e1/q and e2/q (see R.F.C. Walters, Alternate derivation of some regular continued fractions, J. Austr. Math. Soc 8 (1968), 205-212). We used a result of D.N. Lehmer Arithmetical theory of certain Hurwitzian continued fractions, Amer. J. Math. 40 (1918) 375-390.
While enthused with this area, I wasted much time trying to find closed forms for a ratio of series formula for continued fractions such as [1,1,2,2,3,3,..], whose terms increase rapidly enough to allow applying Tannery's theorem (see §63, page 161, Advanced Calculus by G.A. Gibson, MacMillan 1954; also the February 2002, Volume 109, 196-200 AMM article by Josef Hofbauer) to a limiting form of the Euler-Minding formula (see O. Perron, Kettenbrüche, Seite 9.)
(The paper was based on the simple observation (pointed out to me by Barry Jones) that the eigenvalues of PP* and P*P are the same, apart from zeros. The well-spaced numbers property then immediately leads via Gershgorin's theorem, to a Large Sieve estimate previously obtained by K.F. Roth.)
(Using both of Hilbert's inequalities, the Large Sieve estimate N+4.2Δ-1 is obtained. H.L. Montgomery and R.C. Vaughan used the duality idea and subsequently obtained the estimate N+Δ-1 in The large sieve, Mathematika 20 (1973), 119-134.)
This was an attempt to extract arithmetic information from the dual form of the Large Sieve inequality. The result was a version of Selberg's upper bound sieve estimate and is also to be found in Duality in Analytic Number Theory, P.D.T.A. Elliot, Cambridge Tracts in Mathematics 122, CUP 1996. The result was also obtained independently by Isamu Kobayashi, A Note on the Selberg Sieve and the Large Sieve, Proc. Japan Acad. 49 No. 1 (1973) 1-5.) Recently it resurfaced at Joni's Math Notes. Also see a more general version in Arithmetical Aspects of the Large Sieve Inequality, Olivier Ramaré, D. Surya Ramana, inequality (11.36), page 104.
In 1973, G.-C. Rota gave a talk at Nottingham University and I realised that a certain density formula that arose in my Artin conjecture work was an example of a chromatic polynomial of a geometric lattice.
(The above power residues problem led me to study the Crapo-Rota formulation of the 4 colour problem and its dual. I wasted some time trying to prove the four colour problem. I did stumble on the above graph theory result, however. It gets a mention in the book Integer Flows and Cycle Covers of Graphs, Cun-Quan Zhang, Monographs and Textbooks in Pure and Applied Mathematics 205, Marcel Dekker 1997
The eulericity e(G) of a bridgeless graph G is the least number of eulerian subgraphs of G which together cover the edges of G. A 1-1 correspondence is shown to exist between the k-tuples of eulerian subgraphs of G and the proper flows mod 2k on a given network based on G. The inequality e(G) ≤ 3 then follows from a result of F. Jaeger. A planar bridgeless graph G is 4-colourable if and only if e(G) ≤ 2.)
(On reading P. Billingsley's Ergodic Theory and Information Theory, I noticed some ergodic similarity between the 3x+1 type mappings and the continued fraction algorithm. Tony Watts introduced me to exact integer programming in HPL Basic.)
(We realized that the observed frequencies of occupation of congruence classes (mod m) by apparently divergent trajectories, were components of stationary vectors of certain Markov matrices Q(m) associated with T. The general case was subsequently investigated by G.M. Leigh, A Markov process underlying the generalized Syracuse algorithm, Acta Arith. 46 (1985) 125-143.)
Two non-trivial 3x+1 type mappings on ℤ2[x] revealed that the conjectural situation is more complicated than for ℤ. The paper's readabilty would have been improved by adding the two pictures on page 22 of the book chapter.
(A discrete version of Newton's method which gives the integer part of (p/q)1/m . Also in H. Lüneburg's book On the Rational Normal Form of Endomorphisms 1987, B.I. Wissenschaftsverlag, Mannheim/Wien/Zürich. See BCMATH program. It was Harley Flanders who supplied the idea of using equation (4).)
Misprints:
- On line -1 of page 175, replace "in base" by "with".
- In the proof of the Lemma, the phrase "But c > x implies" should be replaced by "But c < x implies".
(Bob Buttsworth proved my conjecture that the irreducible parts of the Markov matrices Q(m) arising from the 3x+1 mapping were primitive. The method was capable of generalisation and allowed us to get detailed information about the ergodic sets for T of relatively prime type.)
(This paper describes the structure of ergodic sets for mappings T of relatively prime type. Measures corresponding to observed frequencies of occupation of congruence classes by iterates of T, are constructed on the polyadic numbers, with T being ergodic with respect to each measure.)
(This work would not have been done without the help of my CALC and gnubc programs. These strongly suggested that the smallest multipliers for the extended gcd problem of consecutive Fibonacci numbers were unique and explicitly describable by formulae involving the integer part symbol. Marc Metchnik helped with the numerical investigation.)
Correction: page 206, line -5, the last minus sign should be (-1)m-1.
Our aim was (a) getting small multipliers for the extended gcd problems and more generally (b) unimodular transformation matrices with small entries for the Hermite normal form of an mxn integer matrix A. The algorithms were arrived at by studying limiting versions of LLL applied to [Im|NnA1|···|NAn] as N gets large. Our algorithm is mentioned in the recent book Lattice Basis Reduction: An Introduction to the LLL Algorithm and Its Applications, Murray R. Bremner, CRC Press 2011.
Also see the generalization to the equation Ax2-By2=N in integers, where A > 0, B > 0 and D=AB is not a perfect square and gcd(A,B)=gcd(A,N)=1.
A constructive version of a theorem of Thue is used to provide representations of certain integers as x2-Dy2, where D=2,3,5,6,7.
Addenda and corrigenda.
- I omitted to say on page 1284 that in Case 1 (i), we also have "
".
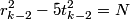- On line -15, "1(a)(2)"" should read "1(i)(a)(2), 1(ii)(b)". Also insert "
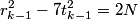" before the last "and".
See corrections and addenda.
Correction. On page 7, line 2, "≤" should be replaced by "<".
Here are the first 1000 partial quotients of the continued fraction expansion of log23.
Mid-point criteria for solving Pell's equation in terms of the nearest integer continued fraction expansion of √D were derived by H.C. Williams using properties of singular continued fractions. We derive these criteria without the use of singular continued fractions.
We derive midpoint criteria for Pell's equation x2-Dy2=±1, using the nearest square continued fraction expansion of √D. The period of the expansion is on average 70% that of the regular continued fraction. We also derive similar criteria for the diophantine equation x2-xy-((D-1)/4)y2=±1, where D ≡ 1 (mod 4). We also present some numerical results and conclude with a comparison of the computational performance of the regular, nearest square and nearest integer continued fraction algorithms.
(i) Misprint: the second equation in equation (2.1), page 486 should read:
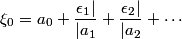instead of
.
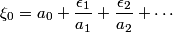(ii) In Lemma 2, page 490, ξv+1 should be ξv-1.
We present a test for determining whether a real quadratic irrational has a purely periodic nearest square continued fraction expansion. This test is somewhat more explicit than the standard test and simplifies the programming of the algorithm.
We prove equality of the period-lengths of the nearest integer continued fraction and the nearest square continued fraction, for arbitrary real quadratic irrationals, using inequalities for approximation constants Θn due to Bosma and Kraaikamp.
We describe the period structure of the optimal continued fraction expansion of a quadratic surd, in terms of the period of the nearest square continued fraction expansion. The analysis results in a faster algorithm for determining the optimal continued fraction expansion of a quadratic surd and has been implemented in a BCMATH program.
We investigate positive solutions (x,y) of the Diophantine equation x2 – (k2+1)y2 = k2 which satisfy y < k-1, where k ≥ 2. It has been conjectured by Andrej Dujella in 2009 that there is at most one such solution for each k. See slidetalk given at the ANU on 30th November 2012.
This finds the primitive solutions of the diophantine equation, using a neglected continued fraction method of Lagrange. See Oeuvres de Lagrange, 725-726. Correction: line 5, page 9. Change second occurrence of "Am" to "Am+1".
Nagell gave upper bound estimates for the fundamental solutions of x2-dy2=N, where d > 1 is nonsquare and N ≠ 0. These were generalized by Bengt Stolt to the diophantine equation Ax2 + Bxy + Cy2=N, D = B2 - 4AC > 1 and nonsquare, A > 0, N ≠ 0. Our paper gives a refinement of Stolt's estimates, which results in a characterization of the fundamental solutions.
We extend theorems of Serret and Pavone for solving ax2 + bxy + cy2 = μ, where a > 0, gcd(x,y) = 1, y > 0. Here d = b2 – 4ac > 0 is not a perfect square and 0 < |μ| < ½√d. If μ > 0, Serret proved that x/y is a convergent to ρ = (-b + √d)/2a or σ = (-b – √d)/2a. If μ < 0, we are able to modify Pavone's approach and show that with at most one exception, the solutions are convergents to ρ or σ. Here is a BCMATH program for finding the fundamental primitive solutions.