MSc thesis, Keith Matthews, University of Queensland, 1966
- Polynomials in an indeterminate t over [q].
Elementary properties of factorisation. Estimate for
the divisor function.
Congruence. Complete and reduced sets. The group G(H,[q]).
Field property mod P. Sums involving multiplicative functions.
- Formal Laurent series over [q].
Field property. Valuation function. Dirichlet diophantine approximation lemma.
- Trace function.
Additive properties. Evaluation of 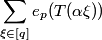 . The functions τs,k(α) and Sξ,[q].
. The functions τs,k(α) and Sξ,[q].
- The function e(Λ).
Evaluation of 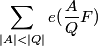 . Formula for r(N) in terms of S(Λ).
. Formula for r(N) in terms of S(Λ).
- Characters and generalised exponential sums.
The equation xd=ξ over [q]. Gaussian sums. Estimation of |Sξ,[q]| and |SA,P|.
- Farey dissection.
Properties of major arcs MF,G and minor arcs mF,G. Explicit determination of MF,G.
- Estimate for S(A/Q) on a minor arc.
Analogue of Weyl's lemma and its application to S(A/Q).
- Estimate for r1(N), the contribution of the minor arcs.
Analogue of Hua's lemma and its application to r1(N).
- Evaluation of S(A/Q) on a major arc.
Relation of S(A/Q) to SF,G and S(Λ). An important property of S(Λ).
- Formula for r2(N), the contribution of the major arcs.
- Estimates for |SF,G|.
Absolute convergence of the singular series.
- The asymptotic formula for r(N).
- The singular series ℭ(N).
- The analogue of Waring's theorem.
- An outline for obtaining χ(P) > 0 under the weaker condition p > k.
Last modified 15th March 2024
. The functions τs,k(α) and Sξ,[q].
. Formula for r(N) in terms of S(Λ).