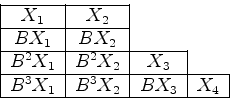A Simple Jordan Canonical Form Algorithm

This document is intended for anyone who has been exposed to a second course in linear algebra and who has been mystified by the usual lengthy treatments of the Jordan canonical form and who simply wants an algorithm which can be implemented by an exact arithmetic matrix calculator such as my CMAT. We omit proofs and present such an algorithm for finding a nonsingular matrix P such that P^-1AP=J_A, the Jordan canonical form of A. (Proofs can be found in my 1991 MP274 lecture notes.)

Motivation

Let A be an n x n matrix over a field F and let the characteristic polynomial ch_A(x) split completely as a product of linear factors over F. Let c be an eigenvalue of A having algebraic multiplicity a and geometric multiplicity g. Then A is similar to a direct sum of elementary Jordan matrices; that is matrices J_e(c), with c on the diagonal, 1 on the subdiagonal and 0 elsewhere.
Let B = A - cI_n. Also let N(B^h) stand for the null space of B^h. Then N(B) and N(B^a) are the eigenspace and generalized eigenspace of A, corresponding to the eigenvalue c.
Let n_h=dim(N(B^h)). Then g=n₁ <= n_a=a. If g=a for all eigenvalues, then J_A is diagonal and there are no difficulties. However if g < a, the situation is more complicated.

Our aim is to choose a basis for N(B) having the form

B^e₁-1X₁, . . . , B^e_g-1X_g, (1)

where e₁>= · · · > e_g>=1 and e₁+ · · · +e_g=a.
For then the following generalized eigenvectors:

X₁, BX₁, . . . , B^e₁-1X₁;

·
·
·
X_g, BX_g, . . . , B^e_g-1X_g

will together form a basis for the generalized eigenspace N(B^a). (See for example either the aforementioned MP274 notes or Lemma, p. 308, Linear Algebra, S.H. Friedberg, A.J. Insel, L.E. Spence, Prentice-Hall 1979.)
Then if P_c is the matrix whose columns are formed from the above list, we have

AP_c = P_cdiag(J_e₁(c), . . . , J_{e_g}(c)).

We then let P be the result of juxtaposing the P_c for the distinct eigenvalues. Then P will be a nonsingular n x n matrix and P^-1AP=J_A.

It helps to visualize the generalized eigenvectors in the following tabular form:

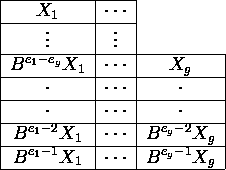
If e₁,...e_k are the exponents >= h, the vectors B^e₁-1X₁, . . . , B^e_k-1X_k, can be shown to form a basis for N_h, the intersection of C(B^h-1) (the column space of B^h-1) and the eigenspace N(B).
In fact k = n_h - n_h-1.

The numbers e₁, . . . , e_g are called the Segre characteristic for the eigenvalue c and form a "vertical" partition of the algebraic multiplicity a. The numbers n_h increase strictly and then become equal:

n₁<· · · < n_b = · · · = n_a = a.

Here b=e₁.
The numbers µ_h = n_h - n_h-1 decrease monotonically:

µ₁ = n₁>=· · · >= µ_b

and are called the Weyr characteristic for the eigenvalue c and form a "horizontal" partition of a.

We remark that the vectors B^jX_i,i=1,...,g, j=0,...,e_i-1, form a basis for N(B^h).

The construction

The above discussion shows that the subspaces N_h hold the key to the construction of the basis (1). We start with a basis for N_b and extend to bases of the successive distinct N_h, until a basis is obtained for N₁ of the form (1). The process is facilitated by the observation that

N_h = < B^h-1Y₁, . . . , B^h-1Y_r >,

if Y₁, . . . , Y_r is a basis for N(B^h). We also make use of the "Left-To-Right" algorithm, which selects a basis from a list of spanning vectors.

An example

Let ch_A(x)=x¹¹. Also suppose that n₁ = 4, n₂ = 7, n₃ = 9, n₄ = 11.
Then µ₁ = n₁ = 4, µ₂ = n₂ - n₁ = 3, µ₃ = n₃ - n₂ = 2, µ₄ = n₄ - n₃ = 2.
Also B=A and our table of generalized eigenvectors is

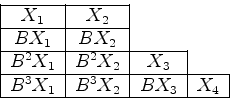
A basis for N₄:: N(B⁴) = <Y₁, . . . , Y₁₁> and hence N₄= < B³Y₁, . . . , B³Y₁₁>.
The Left-To-Right algorithm will give: N₄= < B³X₁, B³X₂>.
A basis for N₂:: N(B²) = <Z₁, . . . , Z₇>, so
N₂= < BZ₁, . . . , BZ₇> = < B³X₁, B³X₂, BZ₁, . . . , BZ₇>.
The Left-To-Right algorithm gives: N₂= < B³X₁, B³X₂, BX₃>.
A basis for N₁:: N(B) = <W₁, . . . , W₄> = < B³X₁, B³X₂, BX₃, W₁, . . . , W₄>.
The Left-To-Right algorithm gives: N(B) = < B³X₁, B³X₂, BX₃, X₄ >.

Then P = [ X₁| BX₁| B²X₁| B³X₁| X₂| BX₂| B²X₂| B³X₂| X₃| BX₃| X₄] has the property that

P^-1AP = diag(J₄(0), J₄(0), J₂(0), J₁(0)).

Added 27th June 2007: The book Matrix Theory by Robert Piziak and Patrick L. Odell, Chapman and Hall/CRC Press 2007, also presents an approach to the Jordan canonical form via the subspaces N_h on pages 389-429.

Last modified 28th May 2021