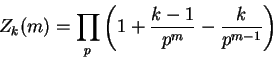 ,
,
The motivation for this thesis was a problem of Hooley [7] communicated by M.N. Huxley in 1976. Huxley pointed out that the existence of a natural density H(a) of primes p for which a is the least primitive root (mod p) follows from Matthews [10] using inclusion-exclusion. He also suggested that it might be possible to prove H(a) positive if a were not perfect power, directly from the resulting complicated formula.
The problem is solved in the latter part of chapter 4 by a general theory of positivity of such sums developed in chapter 1. (H. Lenstra had pointed out (private communication to Dr. K.R. Matthews, 1977) that the results of Lenstra's paper on Artin's conjecture [9] enable one to prove the positivity of H(a), by proving positivity for a suitably chosen subset of primes by applying corollary 4.8 of [9].)
In chapter 1 of this thesis, notation is introduced whereby one considers functions defined on subsets, together with a differencing operator which generalises ordinary differencing in one variable.
The theory of chapter 1 is applied initially in chapter 2 to a problem concerning m-tuples of positive integers. It is well-known that the m-tuples with highest common factor 1 have asymptotic density 1/ζ(m) (see Cesàro [4], Lehmer [8], Nymann [12], Sylvester [13]). Starting from the observation that the subset consisting of those m-tuples for which k prescribed (m-1)-tuples have highest common factor 1, has density
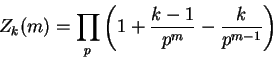 ,
,
the method of chapter 1 is applied to such products to prove that the set of relatively prime m-tuples, such that every (m-1)-subtuple fails to be relatively prime, has a positive density given by the following alternating sum
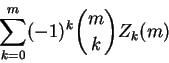 .
.
In the course of considering this problem, a generalisation of the Cesàro etc. problem was derived. Explicitly, in chapter 3 it is proved that given polynomial functions f1,...,fm will have highest common factor h for values of the variables x1,...,xm forming a set whose asymptotic density is
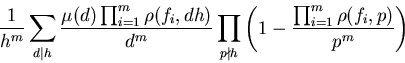 ,
,
where ρ(f,k) denotes the number of solutions of f(x) ≡ 0 (mod k).
(For the special case where f1(x) = ··· = fm(x) = x and h = 1, this formula reduces to ∏p(1 - 1/pm) = 1/ζ(m).)
In the first part of chapter 4, a modification of the Hooley problem is solved, where a is prime. More generally, if S is a given set of primes and p is a prime, then Mp(x,S), the number of primes q not exceeding x for which p is the least member of S which is a primitive root (mod q). is given by
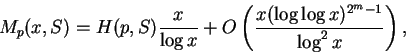 ,
,
where H(p,S) is a positive number independent of x, while m is the number of primes in S less than p. (The result in conditional on the truth of certain Riemann hypotheses for certain Kummer fields.) The reader is prepared for the more general and complicated results of the latter part of chapter 4, where the general problem of Hooley is solved.
Finally it will be obvious that the methods of chapter 4 generalise to several simultaneous primitive roots specified as the only ones less than a given upper bound.
The first part of chapter 1 is published as [3], while chapter 3 is [2] with minor alterations.
6th July 2006