These are downloadable as a gzipped tar file.
They may contain bugs, both on the algorithmic and programming side.
- gcd:
- sign(n).
- abs(n).
- mod(a,b), (b > 0): returns a(mod b).
- int(a,b): returns the integer part of a/b, b nonzero.
- gcd(m,n).
- gcd1(m,n): gcd(m,n)=gcd1(m,n)·m+gcd2(m,n)·n.
- gcd2(m,n).
- lcm(m,n).
- inv(a,n): returns the inverse of a mod m.
- cong(a,b,m): solves ax ≡ b (mod m).
- chinese(a,b,m,n): solves x ≡ a(mod m) and x ≡ b(mod n).
- gcda(m[],n): finds gcd(m[0],...,m[n-1]) and expresses it
as a linear combination of m[0],...,m[n-1].
- lcma(m[],n): finds lcm(m[0],...,m[n-1]).
- chinesea(a[],m[ ],n): solves x ≡ a[i](mod m[i]), i=1,...,n-1.
- chineseb(a[],b[],m[],n): solves a[i]x ≡ b[i](mod m[i]),
i=1,...,n-1.
- mpower(a,b,c): returns ab (mod c).
- exp(a,b): returns ab.
- mthroot(a,b,m): returns the integer part of the mth-root of a/b.
Here a,b and m are positive integers, m > 1. (See K.R. Matthews, Computing mth roots, College Mathematics Journal 19 (1988) 174-176.)
- mthrootr(a,b,m,r): this gives the mth-root of a/b
truncated to r places.
- binomial(n,m): returns the binomial coefficient.
- gcd3(a,b,c): returns gcd(a,b,c).
- ceiling(a,b): returns least integer x>= a/b.
- bezout(a,b), when a and b are non-negative, returns d = gcd(a,b) = globalu*a + globalv*b, where globalu and globalv are global variables. bezout1(a,b) deals with arbitrary integers a and b.
- nearestsquare(d) returns the nearest square to a nonsquare d.
- euclid0: euclid0(m,n) performs Euclid's algorithm and finds the partial quotients and convergents for the continued fraction of m/n, n> 0.
- euclid: euclid(m,n) performs Euclid's algorithm.
- euclid1: euclid(m,n) returns the length of Euclid's algorithm.
- jacobi:
- jacobi(m,n) calculates the Jacobi symbol
- peralta(a,p) finds a square root of a quadratic
residue a mod p, using an algorithm of Rene Peralta.
- serret: serret(p) expresses a prime of the form
4n+1 as the sum of two squares using Serret's algorithm.
- 3x+1: collatz(n) tests the 3x+1 conjecture.
- 3x+371: s(n) tests the 3x+371 conjecture.
- phi: (slow-uses Brent-Pollard only)
- omega(n) returns the number of distinct prime factors of n.
- phi(n) returns the value of Euler's function.
- tau(n) returns the number of divisors of n.
- sigma(n) returns the sum of the divisors of n.
- mu(n) returns the value of the Mobius Function.
- lprimroot(p) returns the least primitive root mod p.
- orderm(a,m) returns the order of a mod m.
- factors: factor(n) attempts to factor n using
Brent-Pollard (slow).
- lucas: lucas(n) performs the strong base 2
pseudoprime test and Lucas pseudoprime test on n. lucasnonverbose(n) is the non-verbose version of lucas.
(Needs jacobi).
- decimal: period(m,n,b) outputs the period
digits of the base b expansion of m/n, where m,n,b (b > 1) are
positive integers, 1≤m < n.
- pell: pell(d,e) finds the least solution of Pell's
equations x2-d*y2=±1,±2,±3 and least primitive solution of x2-d*y2=±4. If e=1, the complete and partial quotients are printed; if e=0, this detail is suppressed.
- surd: surd(d,t,u,v) finds the continued fraction
expansion of a quadratic irrational (u+t√d)/v, where d > 1 is not a square, t,u,v integers, v nonzero.
- unit: unit(d) finds the fundamental unit of
Q(√d).
- fibonacci: f(m,n) prints the Fibonacci numbers
F(m),...,F(n). l(m,n) prints the Lucas numbers L(m),...,L(n).
- rootd: root(d) finds the continued fraction
expansion of √d.
- cfrac: cfrac(m,n) finds the continued fraction
expansion of m/n.
- proth: proth(h,m) investigates the primality of
h*2m+1, h < 2m, using Proth's test.
(Needs jacobi,lucas).
- pollard: pollard(n) attempts to find a factor
of n using the Pollard p-1 method.
- challenge: s(n) tests another 3-branched
generalized 3x+1 conjecture.
- mordell: f(a,k) finds the integer solutions of
y2=x3+a with x ≤ k. (Needs gcd.)
- 4_branch: s(n) tests a 4-branched generalized 3x+1 function.
- venturini1: s(n) tests a 6-branched generalized
3x+1 function of G. Venturini.
- lra: (needs gcd)
- lnearint(m,n) returns the (left) nearest integer to m/n.
- rnearint(m,n) returns the (right) nearest integer to m/n.
- lmodd(m,n) returns the (left) least remainder of sign(n)m mod |n|.
- rmodd(m,n) returns the right) least remainder of sign(n)m mod |n|.
- lra(m,n) performs the least remainder algorithm on m, n.
- nicf(m,n) prints the nearest integer continued fraction of m/n:
m/n = [a0 - 1/a1 - ··· - 1/an].
We write this as (a0,a1,...,an).
- convergents: pn(a[],n) and qn(a[],n) compute the numerator and denominator of the continued fraction [a[0];a[1],...,a[n]].
- lagrange: lagrange(a[],n,m)
uses the method of Lagrange (1797) to find the first m+1 partial
quotients of t, where f(x)=a[n]xn+···+a[0], a[n] > 0, is a polynomial with integer coefficients, having no rational roots
and having exactly one real positive root t, this being > 1.
- lupei: s(n) tests Lu Pei's 3-branched generalized 3x+1 mapping.
- recursion (Recursive bc programs)
- fib(n): returns the nth Fibonacci number, n ≥ 0.
- luc(n): returns the nth Lucas number, n ≥ 0.
- fac(n): returns factorial(n) if n ≥ 1.
- tonelli: x=tonelli(a,p) returns a square root of a (mod p), deterministically.
- discrete_log: r=shanks(n,g,p).
Here g is a primitive root (mod p) and gr ≡ n (mod p), 0 ≤ r < p-1.
Note: p < 232-216=4294901760, in order to satisy BC array upper bound length of 216-1.
If r does not exist, we return -1.
We use Shanks' giant steps-baby steps approach as described in Algorithmische Zahlentheorie by Otto Forster, pp 65-66.
- forster_log: r=shanks(n,g,p).
Similar to discrete_log, except that p is no longer necessarily a prime. Now needs phi to provide orderm(a,m).
- leastqnr: leastqnr(p) returns np, the least quadratic nonresidue mod p. (Needs gcd).
- rootd_modn: rootd_modn(d,n) finds all solutions of the congruence x2 ≡ d (mod n) with 0 ≤ x ≤ n/2 for small n.
- thue: Here d>1, is not a square, n > 1 an odd integer not dividing d-1. u2 ≡ d (mod n), 1 < u < n. Then thue(d,u,p) finds x,y such that x2-dy2=kn, with small k.
- sqroot: sqroot(d,n), n > 1, finds all solutions of x2 ≡ d (mod n). It returns -1 if there is no solution, otherwise returns the number of solutions (mod n).
- tomas1 and tomas2: These are generalised 3x+1 examples studied by Tomás Oliveira e Silva, where all trajectories are eventually periodic.
- log: log(a,b,d,r,e) performs a discrete variant of Shank's logba algorithm. Here 1 < r is an integer. Also d > 1. We do not guarantee the correctness of the output. Bigger (d,r) give more partial quotients. e=1 prints the A[i] and AA[i], while e=0 prints only the m[i] and mm[i]. See paper.
I suggest the user runs test(a,b,d,m,n), over a range (m,n), where m ≤ n, to get an idea of the correct partial quotients. This
runs log1(a,b,d,r) for r=m,...,n.
To get an idea of the correct answer when m=n=r, we recommend taking m=r-t, n=r+t, with 1 ≤ t ≤ (say) 2.
- base: f(b,n), n > 0, b > 1, gives the base b expansion of n.
- perfect_power: perfect_power(n) produces 0 if n is not a perfect power; otherwise returns x and p, where n=xp and p is the least prime with this property.
- powerdd: powerdd(a,b,d,n) computes (a+b√d)n=z1+z2√d, with global variables z1 and z2. It also contains fund4(d,e) which finds the fundamental solution of x2 – dy2 = 4.
- primes: primes(m,n) prints the primes in the interval [m,n], if m and n lie between 1 and 1010.
- nprime: nprime(m) finds the least Lucas-base2 strong pseudoprime p satisfying p ≥ m.
- nprimeap: nprimeap(m,a,b) finds the least Lucas-base2 strong pseudoprime p of the form p=ak+b and satisfying p ≥ m. Here 0 < b < a and gcd(a,b)=1.
- sturm: sturm(a[],n,b,e) prints a sturm polynomial sequence for the (squarefree) polynomial a[n]xn+···+a[0], evaluates the sequence at x=b and calculates its sign variation. e=0 suppresses printing.
- john: johna(b[],n) takes an array of positive integers b[0],...,b[n-1] and replaces them by an array of positive integers a[0],...,a[n-1], where
- a[i] divides b[i] for 0 ≤ i < n;
- gcd(a[i],a[j])=1 for 0 ≤ i < j< n;
- lcm(b[0],...,b[n-1])=a[0]·a[1]···a[n-1].
john(a,b) does the case n=2.
The program is due to John Campbell. Needs the program gcd.
- reducepos: reduce(a,b,c) takes as input an indefinite binary quadratic form ax2+bxy+cy2 and uses the PQa algorithm to find a cycle of reduced forms. (See explanation.)
- classnoneg: class_number(d,flag,table_flag) lists the reduced binary quadratic forms of negative discriminant d and returns their number h(d) if flag=0. If flag=1, only the primitive forms are counted. Only the class number is printed if table_flag=0.
If d is the discriminant of an imaginary quadratic field K, then the primitive forms class-number h(d) is also the class number of K.
Algorithm 5.3.5 of Henri Cohen's A course in computational algebraic number theory is used.
table(m,n) prints h(-d) for all -d ≡ 0 or 1 (mod 4) in the range 3 ≤ m ≤ d ≤ n,
where n<106.
- reduceneg:
- reduce(a,b,c) takes as input a positive definite binary quadratic form ax2+bxy+cy2 and uses an algorithm of Gauss to find the equivalent reduced form and unimodular transforming matrix.
- compose(a1,b1,c1,a2,b2,c2) composes two positive definite binary quadratic forms, with output reduced. Needs bezout from gcd.
- compose1(a1,b1,c1,a2,b2,c2) nonverbose version of compose(). Needs bezout1 from gcd.
- power_compose(a,b,c,n) outputs (a,b,c)n, where (a,b,c) represents a positive definite form. The output is reduced.
- power_compose1(a,b,c,n) nonverbose version of tt>power_compose(a,b,c,n).
- ordercomposite(a,b,c,flag) computes the order under composition, of the positive definite form (a,b,c). flag =1 is verbose, flag=0 nonvebose. We need phi to supply omega(h(d)) and gcd to supply bezout(a,b).
- classnopos: class_number(d) (1 < d < 106 and squarefree) finds the class number of the real quadratic field Q(√d) and the sign of the fundamental unit. A list of reduced binary quadratic forms corresponding to the ideal classes is also given.
table(m,n) prints h(d) for all squarefree d in the range m ≤ d < n,where n < 106.
class_number0(d) (d > 0, not a perfect square and 0 or 1 (mod 4))
returns the class-number of binary quadratic forms of discriminant d. Also the solubility of x2-d*y2=-4 is determined.
This is basically the same program as class_number(d), except that in
the case of non-solubility of x2-d*y2=-4, we count the form (-a,b,c) as well as (a,b,c), a > 0 and this means we return twice the value that class_number(d) would otherwise have returned. Regarding this point, see G.B. Mathews, Theory of Numbers, pp. 80-81.
- unimodular: unimodular(p,q,r,s) expresses a unimodular matrix A ≠ I2 or U=[0,1,1,0] with non-negative coefficients, as a product of one of the following forms:
P, UP, PU, or UPU, where P is a product of matrices of the form Ua=[a,1,1,0], a>0.
The representation is unique. See Kjell Kolden, Continued fractions and linear substitutions, Arch. Math. Naturvid. 50 (1949), 141-196.
The number n of matrices in the product U0  Un-1 is returned.
Un-1 is returned.
- binomial: binomial_p(n,k,p) finds the power of a prime p dividing the binomial coefficient
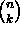 .
.
binomial(n,k) prints the prime power factorization of the binomial coefficient 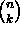 .
.
- factorial: factorial_p(n,p) finds the power of a prime p dividing n!
factorial(n) finds n!
- p-adic:
2adic(a,n) returns the first n binary digits of a 2-adic sqroot x of a positive integer a=8k+1. Here x=1 or 5 (mod 8).
padic(a,p,n) returns the first n p-adic digits of a p-adic sqroot x of a positive integer a which is a quadratic residue (mod p). Here x=b (mod p), where b2=a (mod p) and 0 < b < p.
- raney: raney(p,q,r,s) expresses a nonsingular matrix A=[p,q;r,s] (≠ I_2 or U=[0,1;1,0]) as a product of positive powers of R=[1,1;0,1] and L=[1,0;1,1], followed by a row-balanced matrix D=[a,b;c,d]. ie. a < c & b > d or a > c & b < d. The number of terms L and R is returned.
With Ua=[a,1;1,0], note that
Ua0...Ua2n=Ra0La1...Ra2nU0 and that Ua0...Ua2n+1=Ra0La1...La2n+1I2.
- davison: davison(l,m,n) performs the algorithm of J.L. Davison's paper An algorithm for the continued fraction of el/m, Proceedings of the Eighth Manitoba Conference on Numerical Mathematics and Computing (Univ. Manitoba, Winnipeg, 1978), 169--179, Congress. Numer., XXII, Utilitas Math.
With n ≥ 0, we first find the n* of Davison's Proposition 4.1 and apply Raney's factorisation to A0...Ak, for n* ≤ k ≤ n*+n.
The number (count) of partial quotients of el/m found is returned. count becomes positive for all large n.
- squareroot: This is an improved version of sqroot and contains cornacchia(a,b,m). This finds all positive primitive solutions of ax2+by2=m, where a > 0, b > 0, a+b > m > 0, gcd(a,b)=1=gcd(a,m). If a=b=1, we get solutions with y ≤ x.
r=sqroot(d,n,e) returns the solutions of x2=d (mod n).
r is the number of solutions (mod n).
If e=1, we print the solutions (mod reduced_modulus) as
reduced_solution[0],...,reduced_solution[count-1].
If e=0, solutions are not printed. Used eg. in cornacchia().
If omega(n) > 1, we use the Chinese remainder theorem after solving mod
qglobal[i]kglobal[i], i=0,...,omega(n)-1.
The array solution[0],...,solution[numbr-1] consists of the solutions
(mod n) in the range 0 ≤ x ≤ n/2 and is used in cornacchia().
See A. Nitaj, L'algorithme de Cornacchia, Expositiones Mathematicae 13 (1995), 358-365.
- phi now contains sigmak(k,n) and tau(n), where r=sigmak(k,n), k > 0,n > 0, returns the sum of the k-th powers of the divisors of n and u=tau(n) returns Ramanujan's tau function.
We use the simplest formula for tau(n) given on page 140 of T.M. Apostol, Modular functions and Dirichlet series in number theory, 20-22.
- patz: patz(d,n,e) finds fundamental solutions for the diophantine equation x2-dy2=n, d > 0, d not a perfect square, n ≠ 0 and n ≠ 1.
e=1 is verbose and prints the partial quotients, complete quotients and convergents up to the period (resp. double period) according as the period-length of omega[j] and omega*[j] is even or odd. e=0 prints only the fundamental solutions.
Needs squareroot.
- squareroot now contains quadratic(a,b,c,n,flag). This returns the number k of solutions of the congruence ax2+bx+c ≡ 0 (mod n), where gcd(a,n)=1. The solutions in the range 0 ≤ x < n are returned as global variables quadratic_solution[0],...,quadratic_solution[k-1]. flag=1 prints the solutions.
- patz now contains binary(a,b,c,n). This solves ax2+bxy+cy2=n, where n is non-zero and b2-4ac is positive and not a perfect square. The method is from the paper The Diophantine equation ax2+bxy+cy2=N, D=b2-4ac > 0, Journal de Théorie des Nombres de Bordeaux, 14 (2002) 257-270 by K.R. Matthews.
- decimal2rational.
Typing d2r(pre[],per[],k,r,b) will output the rational number with base b preperiod given by pre[k-1],...,pre[0] (if present) and period per[r-1],...,per[0] consisting of integers in the range [0,b-1].
If there is no preperiod, we let pre[0]=0 and k=0.
Example: Take pre[0]=0, per[0]=2, per[1]=1, k=0, r=2, b=10.
Then typing d2r(pre[],per[],k,r,b) outputs .1212···=4/33.
- sqrtd_period. Typing z=period(d) outputs the period-length z of the continued fraction of √d. We use the Pohst-Zassenhaus half-period trick. See paper.
- nipell. (a) Typing nipell(61,0) finds the smallest solution of Pell equation x2-61y2=1 or -1, using the nearest integer continued fraction of √61. The period (or semi-period in the case that the negative Pell equation is soluble) is also printed.
Typing nipell(61,1) prints partial quotients, complete convergents and convergents.
(b) Typing nicf_pqa(d,t,u,v,e), e=0 or 1, finds the nearest integer continued fraction of (u + t√d)/v of Hurwitz.
Typing nicf_pqa0(d,t,u,v,e), e=0 or 1, finds the nearest integer continued fraction of (u + t√d)/v in Perron's book. When e=1, the period partial numerators and denominators are in capitals.
- nscf_pell. This program solves the Pell equations x2 - dy2 = ±1, using the NSCF algorithm - nearest square continued fraction algorithm. We follow the algorithm of A.A. Krisnaswami Ayyangar.
(a) Typing nscf_pell(d,1) prints the partial quotients, convergents, complete convergents of the period of the nearest square continued fraction of √d, as well as the Pell equation solutions, whereas nscf_pell(d,0) prints only the continued fraction and solutions of the Pell equation.
(b) Typing nscf_pqa(d,t,u,v,e), e=0 or 1, finds the nearest square continued fraction of (u + t√d)/v.
P
- spiral. This calculates the spiral of Concrete Mathematics, Graham, Knuth, Patashnik, Exercise 40, page 99. Needs gcd. Type spiral(n) and then x(n) and y(n) to get the coordinates of the n-th point of the spiral. Typing n=inverse_spiral(x,y) gives the inverse function.
- equivalent. This produces a quadratic surd η=(A+√d)/C=(pξ+q)/(rξ+s), where ξ=(a+√d)/c
and Δ=ps-qr=±1. Here A=Δ(prt+a(qr+ps)+qsc), C=Δ(r2t+2rsa+s^c) and t=(a2-d)/c. If ξ is in standard form, so is η. Type equiv(a,c,d,p,q,r,s).
- carmichael. carmichael(n,e) solves φ(x)=n. e=0 prints all solutions, if any, while e=1 tests Carmichael's conjecture. Needs files phi, lucas, jacobi.
- tangent. Typing tangent(n) produces the n-th tangent number Tn. (8th June 2011)
- bernoulli. Typing bernoulli(n) produces the n-th Bernoulli number. (9th June 2011)
- kronecker. Typing kronecker(d,n) returns the Kronecker symbol (d,n), n ≥ 1.
- partition. Typing partition(m,1) prints the first m values of the partition function p(m)
Typing partition(m,0) returns only p(m). (23rd June 2011)
- cloitre. Typing cloitre(x) prints the trajectory of a mapping devised by Benoit Cloitre, who conjectured that all trajectories starting with a positive integer will eventually reach 0. Experimentally it also seems that all trajectories starting with a negative integer will eventually reach one of the cycles
- -1,-2,-1;
- -4,-17,-6,-4;
- -19,-92,-31,-152,-51,-34,-167,-56,-19.
- cloitrem. Typing cloitrem(m) if m is even or m=4n+1, produces the Markov matrix Q(2m) for the mapping Fm devised by Benoit Cloitre. The mapping is given by typing t(x,m). Finally, typing function(m) produces a listing of the d=2m branches of the mapping in two ways.
- reducepos_zagier. Typing reduce(a,b,c) uses an algorithm from
Don Zagier's book Zetafunktionen und quadratische Körper, Eine Einführung in die höhere Zahlentheorie, to find a reduced form equivalent to (a,b,c) and also prints the cycle this generates.
- zagier. zagier(d) gives the backward continued fraction of √d. zagier0(d,t,u,v) gives the least integer continued fraction of (u + t√d)/v.
- genfacs. Given the canonical factorization p[0]a[0]···p[t-1]a[t-1]of n, typing exps(a[],t) lists the exponent vectors of the divisors of n, whereas typing divisors(p[],a[],t) lists the divisors of n.
- pellab. Typing pellab(a,b,e) solves the diophantine equation ax2-by2=±1 and finds the least positive solution. We assume 1 < a < b, gcd(a,b)=1 and ab is not a perfect square.
- squareroot2. Typing squares(n,flag) finds all representations of n as r2+s2, r<s, gcd(r,s)=1. Here flag=1 is verbose and prints all parts of Euclid's algorithm as in the note. Typing squares1(n) only does that part of Euclid's algorithm as far as rc-1 > √n ≥ rc.
- nagell_test. Typing nagell(d,n) finds the fundamental solutions, if any, of the diophantine equation x2 - dy2 = n, using the bounds given by T. Nagell in his book Introduction to Number Theory, 205-207.
- markoff_triples. Typing test(n) prints all Markoff triples (x,y,z) with x < y < z and 5 ≤ z ≤ n. The recursion is due to Alan Offer.
- patzpos. Typing patzpos(d,n,e), where e=0 or 1 finds the positive fundamental solutions of a generalised Pell equation x2 - dy2 = n, with e = 1 being prolix. The program needs squareroot2.
- primepatterns. Typing primepatterns(a[],b[],s,u,v) will determine if a[0]m+b[0],...,a[s-1]m+b[s-1] form an admissible sequence and if so, will test the absolute values of these numbers for m in the range u ≤ m ≤ v for simultaneous primality. The program needs gcd, lucas, jacobi and a file containing the a[i] and b[i]. Here s ≤ 20.
- posformrep. This solves the diophantine equation bt2+ctu+du2=n, where c2-4bd < 0, gcd(b,c,d)=1 and b > 0. Type bc posformrep squareroot reduceneg and then posrep(b,c,d,a,e), where e = 1 is verbose, e = 0 nonverbose. We use a transformation of variables due to Lagrange (1770) and then reduction to reduced form. See note.
- posformrep2. This solves the diophantine equation bt2+ctu+du2=n, where c2-4bd < 0, gcd(b,c,d)=1 and b > 0. Type bc posformrep2 squareroot and then posrep(b,c,d,a,e), where e = 1 is verbose, e = 0 nonverbose. We use a transformation of variables due to Lagrange (1770) to get an equation Pu2+Quy+Ry2=1 and then perform Euclid's algorithm on -Q/2P. See paper.
- stolt. This finds the fundamental solutions of the diophantine equation ax2+bxy+cy2=n, where d=b2-4ac > 0 is not a perfect square, gcd(a,b,c)=1 and a > 0. Type stolt(a,b,c,n). This is only useful for small d and an. Also typing fund(d,e), e = 0 or 1, finds the least positive solution of Pell's equation x2 - dy2=4,
with e=1 being verbose.
- dujella_minus. The function negdujella1(k) finds all solutions of X2-(k2+1)Y,sup>2= -k2 that lie in the range 1 < Y < k. The Dujella unicity conjecture is equivalent to there being at most one solution. If 2 ≤ m ≤ n, the function test(m,n) performs negdujella1(k) over the range k = m,...,n. We print the solutions (X,Y) and the corresponding solutions (x,y) under the mapping x = (k2+1)Y - kX, y = kY - X. To run the program one needs gcd and squareroot2.
- phi now contains lprimrootneg(p), which finds the least negative primitive root mod p, lprimrootposmn(m,n), which lists the least primitive roots mod p for m ≤ p ≤ n, lprimrootnegmn(m,n), which lists the least negative primitive roots mod p for m ≤ p ≤ n. This need lucas and jacobi..
- wildberger1. This solves Pell's equation x2 - dy2 = ±1 using an algorithm of Norman Wildberger. Type wild(d,e). e = 1 is verbose, e = 0 is nonverbose.
- patz now contains patzgentest(d,n), which lists all fundamental solutions of x2 - dy2 = n and returns the their number. Type bc patz squareroot2 genfacs. Also patzgen creates a global array of these solutions. nagell_test contains ssw0(a,b,c,d,e,f), which solves the diophantine equation ax2 + bxy + cy2 + dx + ey +f = 0, where a ≠ 0, b2 - 4ac > 0 is not a perfect square. These functions are accessed by typing bc patz squareroot2 genfacs nagell_test.
- posformrep now contains posrepgen(a,b,c,n)(d,n), which finds all solutions (primitive and imprimitive) of ax2+bxy+cy2=n as a global array. These are listed by calling posrepgenlist(a,b,c,n). posrepgen(a,b,c,n) is used in ssw1(a,b,c,d,e,f) to solve the diophantine equation ax2 + bxy + cy2 + dx + ey +f = 0, where a ≠ 0, b2 - 4ac < 0. These functions are accessed by typing bc posformrep squareroot2 genfacs reduceneg.
- patz:. Type bc patz squareroot2 genfacs gcd. This now contains
- generalizedpell(a,b,c,e). This solves the diophantine equation ax^2+bxy+cy^2=1, where a is nonzero, d=b^2-4ac>0 and is nonsquare. It produces the global solution class (generalizedpellfundx,generalizedpellfundy).
- binary0(a,b,c,e). This finds the primitive solution classes of the diophantine equation ax2 + bxy + cy2 = n, where d = b2 – 4ac > 0 is not a perfect square, gcd(a,b,c) = 1, gcd(a,n)=1 and n is nonzero. It produces the global solution classes (fund_x[i],fund_y[i]).
- binary1(a,b,c,e). This finds the primitive solution classes of the diophantine equation ax2 + bxy + cy2 = n, where d = b2 – 4ac > 0 is not a perfect square, gcd(a,b,c) = 1, a and n are nonzero. It produces the global solution classes (fund_x[i],fund_y[i]). binary(a,b,c,e) prints these solutions.
binarygen(a,b,c,n,e) This finds all solutions (primitive and imprimitive) of ax^2+bxy+cy^2=n as a global array (globalbinarygenx[i],globalbinarygeny[i]). Here b2 – 4ac > 0, s nonsquare, a and n are nonzero, gcd(a,b,c)=1.
binarygenlist(a,b,c,n,e) prints these classes.
- sswgeneral(a,b,c,d,e,f) . This function lives in patz and solves the diophantine equation ax2 + bxy + cy2 + dx + ey + f = 0, where (a,b,c) ≠ (0,0,0), using a method inspired by a lemma of John Robertson. One needs programs
patz squareroot2 powertest3 genfacs gcd posformrep reduceneg congruence powerdd ddzero-extra arithpartition.bc rob1
This is one of the longest algorithms I have coded in BC and involved updating gcd, powerdd, genfacs, posformrep, reduceneg and constructing the files powertest3 and congruence. Files ddzero-extra and arithpartition.bc were added on December 10, 2019 and incorporate an improvement to the output when D = 0, due to Chi Chon Lei of Imperial College, London.
- inversion. This contains inverse(m,n), which finds the inverse of m modulo n if it exists. The algorithm is from New algorithms for modular inversion and representation by binary quadratic forms arising from structure in the Euclidean algorithm, Christina Doran, Shen Lu and Barry R. Smith.
- b2plus3bcplusc2. This contains rep(p), which expresses a prime of the form 5n+1 or 5n-1 as x2 + xy - y2 and x2 + 3xy + y2. The algorithm is from New algorithms for modular inversion and representation by binary quadratic forms arising from structure in the Euclidean algorithm, Christina Doran, Shen Lu and Barry R. Smith. Type bc lucas gcd b2plus3bcplusc2 jacobi squareroot2 then rep(p).
- patz now contains aa1(a,b,c) and aa2(a,b,c,n). The former solves the diophantine equation ax2-by2=c, using the LMM method, while the latter solves the diophantine equation ax2+bxy+cy2=n, where b2-4ac > 0 and is not a perfect square.
- stolt now contains stolt0(d,n,flag), which solves the diophantine equation x2-dy2=n, n ≠ 0 and a multiple of 4, d > 0 and nonsquare, using inequalities from a paper of Bengt Stolt.
- phi now contains conwaycycles(a,b) and conwaysequence1(a,b,n). See BC program.
- root3 contains cycle(x,y,n), which exhibits the trajectory (x,y), T(x,y), T2(x,y), Tn(x,y), where T is the function defined in Example 10.2., page 101 of
The Ultimate Challenge: The 3x+1 Problem, Ed. Jeffrey C. Lagarias, AMS January 2010. It seems likely that there are 103 cycles and that (x,y) = (-1,7) gives a divergent trajectory. The file gcd is needed.
- partition.bc.
Typing partition(m,1) prints the first m values of the partition function p(m).
Typing partition(m,0) returns only p(m).
Typing strict_partition(m,1) prints the first m values of the strict partition function q(m).
Typing strict_partition(m,0) returns only q(m). Communicated by Thorsten Ehlers, May 3, 2019.
See Computing partition numbers Q(N), an early version of a paper by Evangelos Georgiadis.
- pell1 contains fund1(d,printflag), which finds the fundamental solution (globalr, globals) of Pell's equation x2-dy2 = 1, using the midperiod approach and the continued fraction of √d.
- pell4 contains fund4(d,printflag), which finds the fundamental solution (globalx, globaly) of Pell's equation x2-dy2 = 4, using the midperiod approach and the continued fraction of √d.
- sswgeneral(a,b,c,d,e,f) updated 27th January 2020. This function lives in patz and solves the diophantine equation ax2 + bxy + cy2 + dx + ey + f = 0, where (a,b,c) ≠ (0,0,0), using a method inspired by a lemma of John Robertson. One needs programs
patz squareroot2 powertest3 genfacs gcd posformrep reduceneg congruence powerdd ddzero-extra arithpartition.bc rob1 bigu stoltvialmm stoltarrange.bc
.
- stoltvialmm(d,n,printflag) lives in stoltvialmm and finds the Stolt fundamental solutions of x2 – dy2 = n, where n is divisible by 4.
Needs stoltvialmm stoltarrange.bc squareroot patz genfacs
binaryviasfs(a,b,c,n,printflag also lives in stoltvialmm and finds the stolt fundamental solutions of ax2 +bxy + cy2 = n. This has a wider applicability than the earlier version stolt(a,b,c,n).
- bigu contains bigu(a,b,c,d,e,f,printflag), which solves the hyperbola case of the diophantine equation ax2 + bxy + cy2 + dx + ey + f = 0.
Type bigu(a,b,c,d,e,f,printflag).
Needs bc squareroot bigu stoltvialmm stoltarrange.bc patz genfacs.
- squareroot now contains quadratic(a,b,c,n,printflag).
This returns the number k of solutions of the congruence ax2+bx+c ≡ 0 (mod n), where a,n are positive . The solutions in the range 0 ≤ x < n are returned as global variables
qglobalsol[0],…,qglobalsol[k-1]. printflag=1 prints the solutions. See note.
- gcd now contains rationalization(a,b,c,d,dd), which rationalizes the
denominator in (a + b√dd)/(c + d√ldd).
- Added Ore's method of solving a system of linear congruences x ≡ ai mod (mi).
- November 7, 2024 Added 3x+3korig, which performs the 3x+3k algorithm. Type collatzk(y,k) where k ≥ 1 and y is an integer. The iterates of y will eventually lead to a multiple of 3k, say 3kz, at which point the trajectory becomes 3k times the trajectory of z under the 3x+1 mapping.
Email
http://www.numbertheory.org/keith.html
 Un-1 is returned.
Un-1 is returned.
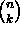 .
.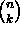 .
.