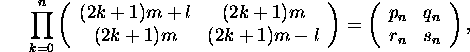Detailed description of the major CALC functions

R0=2¹⁶
USI stands for unsigned int
USL stands for unsigned long
An MPI is a multiprecision integer
An MPMATI is a matrix of multiprecision integers
An MPR is a multiprecision rational
An MPMATR is a matrix of multiprecision rationals
An MPIA is an array of MPI's
A POLYI is a polynomial with MPI coefficients
X is a reserved symbol, for use in polynomials
Stack is used in STURM and also in the wrappers to functions for later use in init.c. It is only in the latter context that I use Stack.

MPI *ABSI(MPI *Aptr): i5m.c

Returns |Aptr|.

void ADD_TO_MPIA(MPIA MA, MPI *V, USL n): i5I.c

Adds the supplied MPI at the subscript n. If slot already exists, the MPI at that slot is freed and the new one is added. If n is greater than the number of slots, then the array is correctly resized and the new MPI is added. Slots between the previous last slots and the new subscript n are initialised to zero.

MPI *ADD0I(MPI *Aptr, MPI *Bptr): i1.c

Returns Aptr+Bptr, Aptr ≥ 0, Bptr ≥ 0.

MPI *ADD0_I(MPI *Aptr, unsigned long b): i1.c

Returns Aptr+b, Aptr ≥ 0, b < R0.

MPI *ADDI(MPI *Aptr, MPI *Bptr): i1.c

Returns Aptr+Bptr.

MPI *ADDM(MPI *Aptr, MPI *Bptr, MPI *Mptr): i5m.c

Returns Aptr+Bptr (mod Mptr), where 0 ≤ Aptr,Bptr < Mptr.

MPMATI *ADDMATI(MPMATI *Mptr, MPMATI *Nptr): i6I.c

Returns Aptr+Bptr.

MPR *ADDR(MPR *Aptr, MPR *Bptr): i5R.c

Returns Aptr+Bptr

void ADD_CUBICR(MPR *X1, MPR *Y1, MPR *X2, MPR *Y2, MPR **Xptr, MPR **Yptr, MPR *A1, MPR *A2, MPR *A3, MPR *A4, MPR *A6): cubicr.c

(Xptr,Yptr) is the sum of the two points (X1,Y1) and (X2,Y2) on the elliptic curve y²+A1·xy+A3·y=X³+A2·X²+A4·x+A6.
See D. Husemoller, Elliptic curves, page 25.

void ADD_ELLIPTIC_Q(MPR *X1, MPR *Y1, MPR *X2, MPR *Y2, MPR **Xptr, MPR **Yptr, MPR *A, MPR *B): elliptic.c

(Xptr, Yptr) is the sum of the two points (X1,Y1) and (X2,Y2) on the rational elliptic curve y²=x³+AX+B, where 4A³+27b² is nonzero.

MPMATI *ADD_MULT_ROWI(USI p, USI q, MPI *Aptr, MPMATI *Mptr): i6I.c

Returns the matrix obtained by adding Aptr times row p to row q of Mptr.

MPMATI *ADD_MULT_ROWI0(USI p, USI q, MPI *Aptr, MPMATI *Mptr): i6I.c

Overwrites Mptr by adding Aptr times row p to row q of Mptr.

unsigned long ADDm(USL a, USL b, USL m): i5m.c

Returns a+b(mod m), where 0 ≤ a,b < m < 2³².

void AXB(): nfunc.c

This solves the linear system AX=B, where the coefficients of A,X,B are integers. A short solution is found in the case of solubility, if N(A) is nontrivial. The method is LLL-based.

void BASE_PADIC(MPI *B, MPI *N, MPIA *BASE, USI *j): p-adic.c

This gives the base B expansion of N > 0.
BASE[]=BASE[0]+BASE[1]B+ ...+BASE[j]B^j.
The integer is returned, along with BASE[]

MPMATI *BASIS_REDUCTION(MPMATI *Bptr, MPMATI **Eptr, USI rowstage, USI m1, USI n1): LLL.c

Input: Bptr, a matrix of MPI's, whose first row is not zero.
Output: an MPMATI whose rows form a LLL reduced basis for the lattice spanned by the rows of Bptr in the sense of the paper "Factoring polynomials with rational coefficients" by A. K. Lenstra, H. W. Lenstra and L. Lovász, Math. Ann. 261, 515-534 (1982).
We use the modified version in "Solving exponential Diophantine equations using lattice basis reduction algorithms" by B. M. M. De Weger, J. No. Theory 26, 325-367 (1987). A change of basis matrix Eptr is also returned.
De Weger's algorithm has been changed to cater for arbitrary matrices whose rows are now in general linearly dependent.
We use the fact that the Gram Schmidt process detects the first row which is a linear combination of the preceding rows. We employ a modification of the LLL algorithm outlined by M. Pohst in J. Symbolic Computation (1987)4, 123-127.
We call this the MLLL algorithm.
The last sigma rows of the matrix Eptr are relation vectors.
(m1, n1) is usually taken to be (3, 4) for a quick answer, but (1,1), while slower, usually provides shorter basis vectors and multiplier.

void BERNOULLI(USL n, MPI **BERNOULLI_NUMERATOR, MPI **BERNOULLI_DENOMINATOR): tangent.c

This calculates the n-th Bernoulli number x/y for n ≤ 4000. See BCMATH description.

MPI *BIG_MTHROOT(MPI *Aptr, unsigned int m): i8.c

The integer part of the mth root of the positive MPI Aptr, 1 < m < R0, is obtained by Newton's method, using the integer part function. (See the article by [Matthews].)

unsigned int BINARYB(MPI *N): binary.c

Returns the number of binary digits of N.

MPI *BINOMIAL(USI n, USI m): i5m.c

returns n choose m, where n ≥ m are unsigned integers.

MPI *BRENT_POLLARD(MPI *Nptr): primes1.c

The Brent-Pollard method returns a proper factor of a composite MPI Nptr. (see R. Brent, BIT 20, 176 - 184).

MPMATI *BUILDMATI(unsigned int m, unsigned int n): i6I.c

Allocates space for an m x n matrix of MPI's.

MPMATR *BUILDMATR(unsigned int m, unsigned int n): i6R.c

Allocates space for an m x n matrix of MPR's.

MPI *BUILDMPI(unsigned int n): i5I.c

Mallocs space for an MPI of length n.
If there is an MPI of this size in the bank, then use it rather than malloc.

MPIA BUILDMPIA(): i5I.c

Allocates space for an array initially of size 11 (enough to hold a[0] to a[10] and sets these slots to contain the zero MPI. Extra MPI's are added using ADD_TO_MPIA.

MPR *BUILDMPR( ): i5R.c

Mallocs space for an MPR.

MPI *CEILINGI(MPI *A, MPI *B): i2.c

Returns the least integer not less than A/B.

MPI *CFRAC_PERIOD(MPI *D): i5I.c

Returns the period of the continued fraction of √D using the half-period approach of Pohst and Zassenhaus.

MPI *CHANGE(unsigned long n): i5I.c

Converts n, 0 ≤ n < (R0)² to an MPI.

MPI *CHANGEI(long n): i5I.c

Converts n, 0 ≤ |n| < R0 to an MPI.

MPI *CHINESE(MPI *A, MPI *B, MPI *M, MPI *N, MPI **Mptr): nfunc.c

Returns the solution mod Mptr=lcm[M,N] and Mptr) of the simultaneous congruences X = A (mod M) and X = B (mod N), if soluble; otherwise returns NULL.

MPI *CHINESE_ARRAY(MPI *A[ ], MPI *M[ ], MPI **Mptr, USI n): nfunc.c

Returns the solution mod Mptr=lcm[M[0],...,M[n-1] and Mptr) of the congruences X = A[i] (mod M[i]),0 ≤ i < n, if soluble; otherwise returns NULL.

MPMATR *CHOLESKYR(MPMATR *A): i6R.c

Input: The positive definite matrix A.
Output: The Cholesky decomposition of A.
(See U. Finke and M. Pohst, "Improved methods for calculating vectors of short length in a lattice, including a complexity analysis." Math. Comp. 44, 463-471, 1985.

MPI *COLLATZ(MPI *Dptr, *Eptr): nfunc.c

The Collatz 3x+1 function. The iterates x,T(x),.. are printed iff Eptr is nonzero.

MPMATI *COLSUBI(USI p, USI q, MPI *Aptr, MPMATI *Mptr): i6I.c

Returns the result of subtracting Aptr times the p-th column of Mptr from the q-th.
0 ≤e p, q ≤ Mprt->C - 1.

MPI *COLSUMI(MPMATI *Mptr, USI j): i9.c

Returns the sum of the elements of column j of Mptr.

int COMPAREI(MPI *Aptr, MPI *Bptr): i1.c

Compares MPI's: Returns 1 if Aptr > Bptr, 0 if Aptr = Bptr, -1 if Aptr < Bptr.

int COMPARER(MPR *Aptr, MPR *Bptr): i6R.c

Compares MPR's: Returns 1 if Aptr > Bptr, 0 if Aptr = Bptr, -1 if Aptr < Bptr.

MPI *CONGR(MPI *A, MPI *B, MPI *M, MPI **N): nfunc.c

Returns the least solution (mod N) of the congruence AX=B(mod M) (and N), where N = M / gcd(A, M); otherwise returns the null pointer.

MPI *CONTENTPI(POLYI Pptr): pI.c

Cptr is the content of the polynomial Pptr.

void CONVERGENTS(MPI *A[], MPI **P[], MPI **Q[], MPI *N): i5I.c

Returns the convergents P[0]/Q[0],...,P[N]/Q[N] to [A[0];A[1],...,A[n]] as arrays P[ ] and Q[ ].

unsigned long CONVERTI(MPI *N): i5I.c

Returns N as an unsigned long, providing 0 < N < 2³².

MPI *COPYI(MPI *Aptr): i5I.c

Returns a copy of the MPI Aptr.

MPR *COPYR(MPR *Aptr): i5R.c

Returns a copy of the MPR Aptr.

MPMATI *COPYMATI(MPMATI *Aptr): i6I.c

Returns a copy of the MPMATI Aptr.

MPMATR *COPYMATR(MPMATR *Aptr): i6R.c

Returns a copy of the MPMATR Aptr.

VOID CORNACCHIA(MPI *A, MPI *B, MPI *M): primes1.c

This prints the positive primitive solutions (x,y) of Ax²+By²=M, where A,B,M are positive integers, with gcd(A,M)=1=gcd(A,B).

void CYCLE(USL d, MPI *m[ ], MPI *X[ ], USL INFINITY, USL RANGE): collatz.c

This function searches all trajectories of the d-branched generalized Collatz function, which start from p, |p| <= RANGE/2 (RANGE an even integer). INFINITY is an upper bound for the size of a trajectory, above which the trajecory is deemed to be divergent. Floyd's cycle finding algorithm is used. Also see survey (pdf) by the author.

USL DAVISON(USL l, USL m, USL N): davison.c

We perform the algorithm of J.L. Davison, An algorithm for the continued fraction of e^l/m, Proceedings of the Eighth Manitoba Conference on Numerical Mathematics and Computing (Univ. Manitoba, Winnipeg, 1978), 169-179, Congress. Numer., XXII, Utilitas Math.

The starting point is a result of R.F.C. Walters in Alternate derivation of some regular continued fractions, J. Austr. Math. Soc 8 (1968), 205-212): If

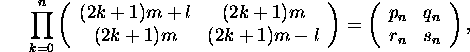
then p_n/r_n and q_n/s_n -> e^l/m
We first find the least n=n* such that p_n,q_n,r_n,s_n are non-negative and repeatedly apply Raney's factorisation for n*≤ k ≤ n*+N, as in Davison's example in §3.
The number (count) of partial quotients of e^l/m found is returned.
We cannot predict the value of count, but it becomes positive for sufficiently large N. We exit if 1,000,000 partial quotients are found.

POLYI DERIV(P): pI.c

Returns the derivative of P.

MPI *DISCRIMINANT(POLYI P): pI.c

Returns the discriminant of P, namely (1/a_n)(-1)^{n(n-1)/2 RESULTANT(P, P').
See O. Perron, Algebra, Vol 1, p.212.

MPI *DIVM(MPI *Aptr, MPI *Bptr, MPI *Mptr): i5m.c

Returns (Aptr / Bptr) mod (Mptr).
Here 0 ≤ Aptr, Bptr < Mptr and gcd(Bptr, Mptr) = 1.

unsigned long DIVm(USL a, USL b, USL m): i5m.c

Returns a / b mod m if m > 0
Here 0 ≤ a, b < m < R0, gcd(b, m) = 1 if m > 0>

MPI *DOTRI(MPMATI *Mptr, USI i, USI j): i7I.c

Returns the dot product of rows i and j in Mptr.

MPI *EFACTOR(MPI *N, USI m, USI p): elliptic.c

The elliptic curve method is used to try to find a factor of a composite number N.
Here m, p < 2³² and 1279 ≥ m > 10, p ≥ 1.

unsigned int EQUALI (MPI *Aptr, MPI *Bptr): i5I.c

Returns 1 if Aptr = Bptr, otherwise = 0.

unsigned int EQUALR (MPR *Aptr, MPR *Bptr): i5R.c

Returns 1 if Aptr = Bptr, otherwise = 0.

unsigned int EQMINUSONECI(MPCI *Mptr): i3.c

Returns 1 if Mptr = -1, 0 otherwise.

unsigned int EQMINUSONECR(MPCR *Mptr): i3.c

Returns 1 if Mptr = -1, 0 otherwise.

unsigned int EQMINUSONEI(MPI *Mptr): i3.c

Returns 1 if Mptr = -1, 0 otherwise.

unsigned int EQMINUSONER(MPR *Mptr): i3.c

Returns 1 if Mptr = -1, 0 otherwise.

unsigned int EQONEI(MPI *Mptr): i3.c

Returns 1 if Mptr = 1, 0 otherwise.

unsigned int EQONER(MPR *Mptr): i3.c

Returns 1 if Mptr = 1, 0 otherwise.

unsigned int EQONECI(MPCI *Mptr): i3.c

Returns 1 if Mptr = 1, 0 otherwise.

unsigned int EQONECR(MPCR *Mptr): i3.c

Returns 1 if Mptr = 1, 0 otherwise.

unsigned int EQZEROI(MPI *Mptr): i3.c

Returns 1 if Mptr = 0, but 0 otherwise.

unsigned int EQZEROR(MPR *Mptr): i3.c

Returns 1 if Mptr = 0, but 0 otherwise.

unsigned int EQZEROCI(MPCI *Mptr): i3.c

Returns 1 if Mptr = 0, but 0 otherwise.

unsigned int EQZEROCR(MPCR *Mptr): i3.c

Returns 1 if Mptr = 0, but 0 otherwise.

MPI *EUCLIDI(MPI *Pptr, MPI *Qptr, MPI **Hptr, MPI **Kptr): nfunc.c

Returns gcd(Pptr, Qptr) = Hptr · Pptr + Kptr · Qptr.

MPI *EUCLIDI1(MPI *Pptr, MPI *Qptr): i5I.c

Returns the length of Euclid's algorithm for Pptr/Qptr.

void EUCLID(MPI *Aptr, MPI *Bptr, MPI **Q[ ], MPI **R[ ], MPI **S[ ], MPI **T[ ], MPI **Dptr)

Returns Q[0]=NULL,Q[1],...Q[n],Q[n+1]=NULL,
* R[0],...R[n + 1],
* S[0],...S[n + 1], T[0],...T[n + 1]
* for Euclid's algorithm on R[0]=Aptr, R[1]=Bptr.
* R[0]=R[1]*Q[1]+R[2]
* R[1]=R[2]*Q[2]+R[3]
* .....
* R[n-2]=R[n-1]*Q[n-1]+R[n]
* R[n-1]=R[n]*Q[n], R[n+1]=0.
* S[0]=1,S[1]=0, S[j]=s[j-2]-Q[j-1]*S[j-1],
* T[0]=0,T[1]=1, T[j]=T[j-2]-Q[j-1]*T[j-1], j=2,...,n+1
* Here *Dptr = n.

MPI *EULER(MPI *N): primes1.c

Returns Euler's function phi(N).

FACTOR(Mptr *Nptr): primes1.c

Attempts to factor Nptr using the Multiple Polynomial Quadratic sieve.
If that fails, it uses the elliptic curve method. (No Peter Montgomery fine-tuning.)
I suggest one uses it for 55 or less digit numbers.

unsigned long *FFI(USL N, USL *b, USL w, USL p): i5m.c

Fast Fourier Interpolation.
Here N is a power of 2, b is an array of N elements from Z_p,
w is a primitive N-th root of unity mod p and N | p - 1.
Outputs a(x)=a[0]x⁰+···+a[0]x^N-1, where a(w^k)=b[k], 0 ≤ k < N.
(See "Elements of Algebra and Algebraic Computing", J.D. Lipson, p.303.
I have been unable to free the arrays B and C, due to the way the recursion works.

unsigned long *FFP(USL N, USL *a, USL *b, USL m, USL n, USL w, USL p): i5m.c

Input: arrays a and b of USL's mod p, representing polynomials
of degrees m, n, respectively; N = 2^e > m + n, N | p - 1. w is a primitive N-th root of unity mod p.
Output: array c mod p, representing a(x)b(x).

MPI *CRA(USL n, USL *a, USL *m): i5m.c

Garner's Chinese Remainder Theorem.
Page 180, Algorithms for computer algebra, K.O. Geddes, S.R. Czapor, G. Labahn.
Here gcd(m[i],m[j])=1 if i != j.
Returns the least remainder mod(m[0].....m[n]) of u = a[i]mod(m[i]), 0 < =i < = n.

MPI *FFM(MPI *a, MPI *b, USL K): i5m.c

Returns the product of a=(a[0],...,a[m])_B and b=(b[0],...,b[n])_B, B=2¹⁶,
m = a->D, n = b->D, using the Discrete Fast Fourier Transform.
Let M = min(m,n). Then a(x)b(x)=c(x), where 0 ≤ c[k] < (M+1)B².
Using the CRA mod fp[i] for 0 ≤ i ≤ K-1, enables us to reconstruct c(B),
provided that fp[0]···fp[K-1] ≥ (M+1)B².
We also need m+n < N = 2^e, where N | fp[i] - 1.
If m <B and n < B, then M < B, then K=3 primes suffice as fp[i]>=B
and we take e>=17.
If m < 2²⁶ and n < 2²⁶, then M < 2²⁶, then K=4 primes suffice and we take e > = 27, N = 2^27.
External variables:
fp[0] = 2013265921, lprimroot[0] = 31, primitive Nth root = 440564289;
fp[1] = 2281701377, lprimroot[1] = 3, primitive Nth root = 129140163;
fp[2] = 3221225473, lprimroot[2] = 5, primitive Nth root = 229807484;
fp[3] = 3489660929, lprimroot[3] = 3, primitive Nth root = 1392672017.
See Elements of Algebra and Algebraic Computing, J.D. Lipson, p.310.
I do not use FFM, as my implementation seems slow. If the user wants to invoke it, go to i1.c and uncomment the relevant parts of MULTI( ).

MPI *FIBONACCI(USI n): functions.c

Returns the nth Fibonacci number.

void FINCKE_POHST(MPMATR *A, MPR *C): i6R.c

Input: A matrix of integers A with LI rows spanning a lattice L.
Output: The integer vectors X with ||X||² ≤ C, highest nonzero coord ≤ 0.
(See Improved methods for calculating vectors of short length
in a lattice including a complexity analysis,
U. Fincke and M. Pohst, Mathematics of Computation, 44, 1985, 463-471.

MPI *FINPUTI(FILE *f, unsigned int *uptr): i5I.c

Converts decimal input from stream into an MPI Mptr.
Ignores the combination '\' followed by '\n'.
If a rubbish character is met before decimal input, Mptr is set to 0
and 0 is returned. All characters up to and including the first newline
met are wiped.
If a rubbish character is met immediately after decimal input,
uptr = 0 is returned and all characters up to and including
the first newline met are wiped. Otherwise 1 is returned.
In any case Mptr is set equal to any inputted decimal.

MPMATI *FINPUTMATI(FILE *infile): i6I.c

Inputs a matrix of MPI's from infile.

MPR *FINPUTR(FILE *f, unsigned int *uptr): i5R.c

Converts the ratio of two decimal inputs from stream into an MPR.
uptr = 0 if input fails, 1 if successful.

void FPRINTI(FILE *outfile, MPI *Mptr): i5I.c

The MPI Mptr is printed in decimal notation to outfile.
No new-line is incorporated.

void FPRINTMATI(FILE *outfile, USI i1, USI i2, USI j1, USI j2, MPMATI *Mptr): i6I.c

Printing an MPMATI to outfile.

void FPRINTMATR(FILE *outfile, USI i1, USI i2, USI j1, USI j2, MPMATR *Mptr): i6I.c

Printing an MPMATR to outfile.

void FPRINTR(FILE *outfile, MPR *Aptr): i5R.c

prints the MPR Aptr as (Aptr->N)/(Aptr->D).

MPR *FRAC_PARTI(MPI *Aptr, MPI *Bptr): i5R.c

Returns the fractional part of Aptr/Bptr.

MPR *FRAC_PARTR(MPR *Aptr): i5R.c

Returns the fractional part of Aptr.

void FREEMATI(MPMATI *Mptr): i6I.c

Frees the storage allocated to the 2-dimensional array Mptr->V.

void FREEMATR(MPMATR *Mptr): i6R.c

Frees the storage allocated to the 2-dimensional array Mptr->V.

void FREEMPI(MPI *Mptr): i5I.c

Deallocates the space alloted for the MPI Mptr.

void FREEMPIA(MPI *Mptr): i5I.c

Frees an MPIA previously returned by BUILDMPIA. It will free all the the MPI's in the MPIA.

void FREEMPR(MPR *Mptr): i5R.c

Deallocates the space alloted for the MPR Mptr.

MPI *FUND_UNIT(MPI *D, MPI **Xptr, MPI **Yptr): nfunc.c

This is a program for finding the fundamental unit of Q(sqrt(D)).
The algorithm is based on:
K. Rosen, Elementary number theory and its applications, p382,
B.A. Venkov, Elementary Number theory, p.62
D. Knuth, Art of computer programming, Vol.2, p359,
with Pohst's trick of using half the period.
w=(1+sqrt(D))/2 if D=1 (mod 4), w=sqrt(D) otherwise.
The norm of the fundamental unit Xptr + Yptr·w is returned.

MPI *GCD(MPI *Aptr, MPI *Bptr): i5I.c

Returns GCD(|Aptr|, |Bptr|).

MPI *GCD_ARRAY(MPI *M[ ], unsigned int n): i5I.c

Returns GCD(M[0], ..., M[n - 1]).

MPI *GCD_ARRAYV(MPI *M[ ], MPI **Y[ ], USI n): nfunc.c

Returns d=gcd(M[0],...,M[n-1]) and an array Y[ ] of MPI's
such that d = M[0]Y[0]+···+M[n-1]Y[n-1]. Here n > 1.

unsigned long GCDm(USL m, USL n): i5m.c

Returns gcd(m,n)>

void GetReturn( ): menu.c

Waits for a return to be entered from the keyboard.

unsigned int GetYN( ): menu.c

Gets a character from the keyboard, making sure it's a
y or an n (either case). If at first the user doesn't succeed,
he/she tries, tries again. 0 is returned if n, 1 if y.

MPI *HALFMOD(MPI *A, MPI *B): i2.c

Here B > 0. Returns R=A(mod B) if R ≤ B/2, otherwise R-B.

MPMATI *HERMITE1(MPMATI *Aptr, USI *T, USI nz): i6I.c

(Kannan-Bachem) Returns the Hermite normal form of Aptr.

MPMATI *HERMITE1P(MPMATI *Aptr, MPMATI *Pptr, MPMATI **Qptr, USI *T, USI nz): i6I.c

(Kannan-Bachem) Returns the Hermite normal form of Aptr and a transforming unimodular matrix Pptr.

MPMATI *IDENTITYI(USI n): i6I.c

Returns the identity matrix of size n.

MPI *INPUTI(unsigned int *uptr): i5I.c

Inputs an MPI from the keyboard.

MPR *INPUTR(unsigned int *uptr): i5I.c

Inputs an MPR from the keyboard.
uptr=1 if no corruption takes place, else 0.

MPMATI *INPUTMATI( ): i6I.c

Inputs a matrix of MPI's from stdin.

MPI *INT0(MPI *Aptr, MPI *Bptr): i2.c

Returns the integer part of Aptr/Bptr,
where Aptr,Bptr > 0.

MPI *INT0_(MPI *Aptr, unsigned long b): i2.c

Returns the integer part of Aptr/b,
where Aptr > 0 and 0 < b < R0.

MPI *INT(MPI *Aptr, MPI *Bptr): i2.c

Returns the integer part of Aptr/Bptr,
where Bptr > 0.

MPI *INT_(MPI *Aptr, USL b): i2.c

Returns the integer part of Aptr/b, 0 < b < R0.

MPI *INTI(MPI *Aptr, MPI *Bptr): i2.c

Returns the integer part of Aptr/Bptr.

MPR *INTR(MPR *Aptr): i5R.c

Returns the integer part of Aptr.

MPI *INVERSEM(MPI *Nptr, MPI *Mptr): i5m.c

Returns the inverse of Nptr (mod Mptr).
Here gcd(Nptr,Mptr) = 1, 1 ≤ Nptr < Mptr.
(See Knuth, p. 325.)

MPR *INVERSER(MPR *Aptr): i5R.c

Returns 1/ Aptr.

unsigned long INVERSEm(USL n, USL m): i5m.c

Returns the inverse of n (mod m).
Here 1 ≤ n < m < 2³², gcd(n, m) = 1.

MPI *JACOB(MPI *M, MPI *N): func.c

Returns the Jacobi symbol (M/N), N odd, N > 0.

int JACOBI(USL n, USL m): qres.c

Returns the Jacobi symbol (n/m), m odd, 0 < n < m.

MPMATI *JACOBIGCD(MPMATI *DD, MPI **Aptr, USI m): LLLGCD.c

Input: an m x 1 vector DD of positive MPI's.
Output: Aptr = gcd of the DD[i]. Also we return a set of
multipliers using a version of a method of Jacobi
A unimodular transforming matrix B is returned.

void LAGRANGE(POLY P, **AA[], MPI *M): i5I.c

f(x)=a[n]xⁿ+···+a[0], a[n] > 0, is a polynomial with integer coefficients, having no rational roots and having exactly one real positive root x, this being > 1. The method of Lagrange (1769) is used to find the the first m+1 partial quotients aa[0],···aa[m] of x. WARNING: the array a[] will be changed after lagrange is called.
Then a further call to lagrange will produce subsequent partial quotients. (See Knuth, Art of computer programming, volume 2, problem 13, 4.5.3.
Also S. Lang and H. Trotter,Continued fractions for some algebraic numbers J. für Math. 255 (1972) 112-134; Addendum 267 (1974) ibid. 219-220.
E. Bombieri and A. van der Poorten, Continued fractions of algebraic numbers, Computational algebra and number theory (Sydney, 1992), 137-152, Math. Appl., 325, Kluwer Acad. Publ.
P. Shiu, Computation of continued fractions without input values, Math. Comp. 64 (1995), no. 211, 1307-1317.

MPI *LCM(MPI *Aptr, MPI *Bptr): i5I.c

Returns lcm(Aptr,Bptr).

MPI *LCM_ARRAY(MPIA M): i5I.c

Returns lcm(M[0],...,M[n - 1]).

MPI *LEASTQNR(MPI *P): qres.c

Returns the least quadratic non-residue mod P.

unsigned long LENGTHI(MPI *Mptr): i5I.c

Returns the number of decimal digits in the MPI Mptr
increased by 1 if Mptr is negative.

unsigned int LENGTHm(USL n): i5m.c

Returns the number of decimal digits in the unsigned int n.

MPI *LENGTHSQRI(MPMATI *Mptr, USI i): LLL.c

Returns the square of the length of row i of matrix Mptr.

MPMATI *LLLGCD(MPMATI *DD, MPI **Aptr, USI m, USI m1, USI n1): LLLGCD.c

Input: an m x 1 vector of MPI's.
Output: gcd of the vector of DD[i]. We return a small set of
multipliers using the LLL method of Havas, Majewski and Matthews.
matrix B of the algorithm is returned.
(m1, n1) is usually taken to be (3, 4) for a quick answer,
but (1,1), while slower, usually provides a shorter basis vectors.

void LOG(MPI *A, MPI *B, MPI *D, MPI *R, MPIA *M, MPI **L): log.c

Returns an array M[] of L positive integers that are hopefully partial quotients of log(A)/log(B), using C=D^R.
Here A > B > 1, D > 1, R ≥ 1.
Uses an algorithm in manuscript

MPI *LPRIMROOT(MPI *P): primes1.c

Returns the least primitive root mod P, an odd prime;
returns NULL if factorization of P - 1 is unsuccessful.

MPI *LUCAS(MPI *N)

Here N is odd, N > 1.
If LUCAS(N) returns 1, then N is a strong base 2 pseudoprime
and a Lucas probable prime; if it returns 0, then N is composite.
(See The Pseudoprimes to 25·10⁹,
Mathematics of computation, 35 (1980) 1003-1026.
At the end of this paper it is conjectured that if N is a strong
base 2 pseudoprime and a Lucas probable prime, then N is in fact a prime.

int MAX(int i, int j): i1.c

int MIN(int i, int j): i1.c

MPI *MAXMPI(MPI *I, MPI *J): i1.c

MPI *MINMPI(MPI *I, MPI *J): i1.c

MPI *MINUSI(MPI *Aptr): i5I.c

Returns -Aptr.

MPR *MINUSI(MPR *Aptr): i5R.c

Returns -Aptr.

MPI *MINUSM(MPI *Aptr, MPI *Mptr): i5m.c

Returns -Aptr (mod Mptr).
Here 0 ≤ Aptr < Mptr.

unsigned long MINUSm(USL a, USL m): i5m.c

Returns -a (mod m) if m > 0.
Here 0 ≤ a < m < 2³².

MPI *MINUS_ONEI( ): i5I.c

Returns -1 as an MPI.

MPR *MINUS_ONER( ): i5R.c

Returns -1 as an MPR.

MPI *MOBIUS(MPI *N): primes1.c

Returns the Mobius function mu(N),
returns NULL if factorization unsuccessful.

MPI *MOD(MPI *Aptr, MPI *Bptr): i2.c

Returns Aptr (mod Bptr), Bptr > 0.

MPI *MOD0(MPI *Aptr, MPI *Bptr): i2.c

Returns Aptr (mod Bptr), Aptr ≥, Bptr > 0.

unsigned long MOD0_(MPI *Aptr, unsigned long b): i2.c

Returns Aptr (mod b), Aptr ≥, 0 < b < R0.

unsigned long MOD_(MPI *Aptr, unsigned long b): i2.c

Returns Aptr (mod b), 0 < b < R0.

unsigned long MODINT0_(MPI *Aptr, unsigned long b, MPI **Qptr): i2.c

Returns Aptr (mod b) and Qptr = int(Aptr/b).
Here Aptr ≥ 0, b is a positive integer, b < R0.

MPI *MPOWER(MPI *Aptr, MPI *Bptr, MPI *Cptr): i5m.c

Returns (Aptr)^Bptr (mod Cptr).
Here Cptr > 0, Bptr ≥ 0.
We use an analogue of the Russian Peasant Multiplication algorithm and conserve the quantity w=zx^y(mod c).
Initially z=1,x=1,y=b.
If y is odd, y → y-1, z → z*x(mod c);
if y is even, y → y/2, x → x²(mod c).
Eventually y=0. Then w=zx⁰(mod c)=z and the final value of z gives a^b(mod c).

MPI *MPOWER_(long a, MPI *Bptr, MPI *Cptr) i5m.c

Returns a^Bptr (mod Cptr).
Here 0 < |a| < R0, Cptr > 0, Bptr ≥ 0.

MPI *MPOWER_M(MPI *Aptr, USL b, MPI *Cptr): i5m.c

Returns (Aptr)^b (mod Cptr).
Here Cptr > 0, 0 ≤ b < RO.

void MTHROOT(MPI *Aptr, MPI *Bptr, unsigned int m, unsigned int r): i8.c

Aptr and Bptr are positive MPI'S. 0 < mr < R0².
The mthroot of Aptr/Bptr is computed to r decimal places, r ≥ 0.

MPR *MTHROOTR(MPR *Nptr, unsigned int m, unsigned int r): i8.c

The m-throot of the positive MPR Nptr is computed to r decimal places,
m, r are integers, r ≥ 0, 0 < mr < R0².

void MULT_PADIC(MPIA A, MPIA B, MPI *P, MPIA *PROD, USI m, USI n, USI *l): p-adic.c

MULT_PADIC forms the product of a=a[0]+a[1]p+...+a[m]p^m
and b=b[0]+b[1]p+...+b[n]pⁿ, where a[m] and b[n] are nonzero.
The output is PROD[0]+PROD[1]p+...+PROD[l]p^l, where PROD[l] is nonzero.
If a or b is zero, we return 0 at the start, otherwise return l.
The program is an adaption of one in i1.c from http://www.numbertheory.org/calc/

MPI *MULTABC(MPI *A, MPI *B, MPI *C): i1.c

Returns A + BC.

MPR *MULTABCR(MPR *A, MPR *B, MPR *C): i1.c

Returns A + BC.

MPI *MULTI(MPI *Aptr, MPI *Bptr): i1.c

Returns Aptr·Bptr;.

MPI *MULTR(MPR *Aptr, MPR *Bptr): i5R.c

Returns Aptr·Bptr;.

MPI *MULTI3(MPI *A, MPI *B, MPI *C): i1.c

Returns ABC.

MPR *MULTR3(MPR *A, MPR *B, MPR *C): cubicr.c

Returns ABC. Here 0 ≤ Aptr, Bptr < Mptr.

MPMATI *MULTMATI(MPMATI *Mptr, MPMATI *Nptr): i6I.c

Returns Mptr·Bptr.

MPMATR *MULTMATR(MPMATR *Mptr, MPMATR *Nptr): i6R.c

Returns Mptr·Bptr.

MPI *MULT_I(MPI *Aptr, long b): i1.c

Returns Aptr·b, where |b| < R0.

MPI *MULT_II(MPI *Aptr, USL b): i1.c

Returns Aptr·b, where b is an USL.

MPI *MULTM(MPI *Aptr, MPI *Bptr, MPI *Mptr): i5m.c

Returns Aptr·Bptr (mod Mptr).

unsigned long MULTm(USL a, USL b, USL m): i5m.c

Returns ab (mod m) if m > 0; here 0 ≤ a,b < m < 2³².

MPI *NEAREST_INTI(MPI *Aptr, MPI *Bptr): i5I.c

Returns the nearest integer to Aptr/Bptr,
choosing downwards if half an odd integer.

MPI *NEAREST_INTR(MPR *Aptr): i5R.c

Returns the nearest integer to Aptr,
choosing downwards if half an odd integer.

MPI *NEG(MPI *d, MPI *FLAG, MPI *TABLE_FLAG): reductio.c

Here d < 0 and 1 < |d| < 10⁶ is squarefree and d=0 or 1(mod 4).
This is Henri Cohen's Algorithm 5.3.5, p. 228, for finding the class number h(d) of binary quadratic forms of discriminant d, when d < 0.
If FLAG=1, we only the primitive forms.
If TABLE_FLAG=0, we do not print any form. This flag was introduced for TABLENEG below.
h(d) is returned in each case.
If d is the discriminant of an imaginary quadratic field K, then the primitive forms class-number h(d) is also the class number of K.
Davenport's Higher Arithmetic has a table of forms, which lists the imprimitive ones with an asterisk.

MPI *NEXTPRIMEAP(MPI *A, MPI *B, MPI *M): utility.c

Finds the first Lucas probable prime P, A | P - B, M ≤ P.
Here A is even, B is odd, A > 1 , A > B ≥ 1, gcd(A,B) = 1, M > 1.

MPI *NEXT_PRIME(MPI *M, USI *hptr): utility.c

Returns a probable prime Q with Q = M + hptr.

MPI *ONEI( ): i5I.c

Returns 1.

MPR *ONER( ): i5R.c

Returns 1.

unsigned int ORDERECP(MPI *X, MPI *Z, MPI *P, MPI *Q, MPI *N): elliptic.c

Calculates the order of the point (X,Y,Z) on the elliptic curve
Y²Z=X³+PXZ²+QZ³ (mod N), N a prime.

MPI *ORDERM(MPI *A, MPI *M): primes1.c

Returns the order of A (mod M).

MPI *ORDERP(MPI *A, MPI *P): primes1.c

Returns the order of A (mod P), P a prime.

void PADICSQRT(MPI *A, USI n, MPI *P, MPIA *DIGITS): p-adic.c

PADICSQRT() n > 0, A > 0, A a quadratic residue (mod P), finds a square-root U of A (mod P), 0 < U < P and returns the first n digits of a p-adic sqroot x of A. Here x=U (mod P). See lectures and solutions.

MPI *PARTITION(USL m): tangent.c

This algorithm is taken from http://www.numericana.com/answer/numbers.htm#partitions and implements a recurrence relation of Euler - see Hardy and Wright, An introduction to the theory of numbers (1962 edition), p. 286 . We calculate p(n) for 1 ≤ n ≤ 65535 = MAX_ARRAY_SIZE - 1.

void PATZ(MPI *D, MPI *N): lagrange.c

Returns the fundamental solutions (x,y) (with x > 0) of x²-Dy²=± N, where D > 1 is not a perfect square and N is non-zero.
The algorithm goes back to Lagrange and has been strangely forgotten by textbook writers. (See the preprint (pdf 173K) of Keith Matthews.)

MPI *PEL(MPI *D, MPI*E, MPI **Xptr, MPI **Yptr): nfunc.c

This finds the least solution of Pell's equation x² - Dy² = ±1.
The algorithm is based on K. Rosen,
Elementary number theory and its applications, p382,
B.A. Venkov, Elementary Number theory, p.62
and D. Knuth, Art of computer programming, Vol.2, p359,
with Pohst's trick of using half the period.
The partial quotients are printed iff E is nonzero.
The norm of the least solution is returned.

void PELL(MPI *Dptr, MPI *Eptr): nfunc.c

This finds the period of the regular continued fraction
of square-root d, as well as the least solution x,y
of the Pellian equation x²-dy²=±1.
The algorithm is from Sierpinski's Theory of Numbers, p.296.
and Davenport's The Higher Arithmetic, p.109.
Here sqrt(d)=a[0]+1/a[1]+···+1/a[n-1]+1/2*a[0]+1/···.
The partial quotients are printed iff Eptr is nonzero.
The length n of the period a[1],···,a[n-1],2*a[0] is printed.

MPI *PERFECT_POWER(MPI *N): primes1.c

If N > 1, this returns X if N=X^k for some X, k > 1, otherwise NULL.

MPI *POLLARD(MPI *Nptr): primes1.c

Pollard's p-1 method of factoring Nptr.

USI POS(MPI *d): reductio.c

This returns the class number h=h(d) of a real quadratic field Q(√d). Here 2 < d < 10⁶ is squarefree and D is the field discriminant. We locate all reduced irrationals of the form (b+\sqrt(D))/(2|c|), where c is negative and 4*c divides d-b². We use the PQa continued fraction algorithm of Lagrange to break the set into disjoint cycles, retaining one number from each cycle. Each reduced number then gives rise to a reduced form (a,b,c) of discriminant D, where a=(b²-D)/(4c).
We are able to also determine if the Pell equation x²-D*y²=-4 has a solution, thereby finding the norm of the fundamental unit.
(See Henri Cohen's A course in computational number theory, page 260, First Edition.)

USI POS0(MPI *d): reductio.c

We find the number of classes of binary forms of positive discriminant d. Here 1 < d < 10⁶. Also d is not a perfect square. We locate all reduced irrationals of the form (b+\sqrt(d))/(2|c|), where c is negative and 4*c divides d-b². We use the PQa continued fraction algorithm of Lagrange to break the set into disjoint cycles, retaining one number from each cycle. Each reduced number then gives rise to a reduced form (a,b,c) of discriminant d, where a=(b²-d)/(4c). We are able to also determine if the Pell equation x²-d*y²=-4 has a solution, by using the fact that the equation is soluble iff at least one of the above cycles is odd. If there is no solution, the reduced forms (-a,b,-c) have to be counted as well. (See G.B. Mathews, Theory of Numbers, 80-81.)
(Also see Henri Cohen's A course in computational number theory, page 260, First Edition.)

USI POS1(MPI *D, *norm): reductio.c

D is squarefree. This function performs Lagrange's method on all reduced quadratic irrationals (b+\sqrt(Disc))/2|c|, where 4*c divides Disc-b², Disc being the discriminant. The class-number h(D) of Q(sqrt(D) is calculated, as well as the norm of the fundamental unit. For use in TABLEPOS(M,N).

void POWERD(MPI *A, MPI *B, MPI* D, MPI *N, MPI **AA, MPI **BB): i2.c

Returns (A+B√D)^N=AA+BB√D.

MPI *POWERI(MPI *Aptr, unsigned n): i1.c

Returns (Aptr)ⁿ, where 0 ≤ n < R0².

MPR *POWERR(MPR *Aptr, unsigned n): i5R.c

Returns (Aptr)ⁿ, where 0 ≤ n < R0².

void POWER_CUBICR(MPR *X1, MPR *Y1, MPR **Xptr, MPR **Yptr, MPR *A1, MPR *A2, MPR *A3, MPR *A4, MPR *A6, unsigned int n): cubicr.c

(Xptr,Yptr)= n(X1,Y1), where 0 ≤ n < R0² and (X1, Y1)
is on the elliptic curve y²+A1·xy+A3·y=X³+A2·X²+A4·x+A6.
(See D. Husemoller, Elliptic curves, page 25.)

MPI *POWER_I(long a, unsigned n): i1.c

Returns aⁿ, where 0 ≤ n < R0².
a is an integer, |a| < R0.

unsigned long POWER_m(USL a, USL y, USL m): i5m.c

Returns a^y (mod m).
Here 0 ≤ a < m < R0 and 0 ≤ y.

unsigned long POWERm(USL a, MPI *Bptr, USL m): i5m.c

Returns a^Bptr (mod m).
Here 0 ≤ a < m < R0 and 0 ≤ Bptr.

MPI *PRIME_GENERATOR(MPI *M, MPI *N): primes1.c

Returns and prints the the c primes, (c ≥ 0), in the interval [m,n], where 1 < m,n < 10¹⁰. Output is sent to primes.out.

POLYI PRIMITIVEPI(POLYI Pptr): pI.c

Returns the primitive part of the polynomial Pptr.

void PRINTI(MPI *Mptr): i5I.c

Prints the MPI Mptr.

void PRINTR(MPR *Mptr): i5R.c

Prints the MPR Mptr.

void PRINTMATI(USI i1, USI i2, USI j1, USI j2, MPMATI *Mptr): i6I.c

Prints the matrix Mptr, rows i1-i2, cols j1-j2.

void PRINTMATR(USI i1, USI i2, USI j1, USI j2, MPMATR *Mptr): i5R.c

Prints the matrix Mptr, rows i1-i2, cols j1-j2.

unsigned long RANDOMm(USL x): i5m.c

input: seed x, output: a "random number" a x + c (mod m).
a = 1001, m = R0 = 65536, c = 65.
From H. Lüneburg, On the Rational Normal Form of Endomorphisms,
B.I. WissenSchaftsverlag, Mannheim/Wien/Zurich, 1987.
See Knuth Vol 2, Theorem A, p. 16.

USL RANEY1(MPI *P, MPI *Q, MPI *R, MPI *S): davison.c

Input: a non-singular matrix A=[P,Q;R,S], P,Q,R,S ≥ 0, A!=I₂, A!=[0,1;1,0].
With L=[1,0;1,1] and R=[1,1;0,1], we express A uniquely as a product of non-negative powers of L and R, (at least one is positive) followed by a row-balanced B.
B=[a,b;c,d] is row-balanced if (a < c & b > d) or (c < a & d > b) and a,b,c ≥ 0.
The number k of powers of L and R is returned. The maximum number of partial quotients returned is 10⁶.

MPR *RATIOI(MPI *Aptr, MPI *Bptr): i5R.c

Returns Aptr/Bptr.

MPR *RATIOR(MPR *Aptr, MPR *Bptr): i5R.c

Returns Aptr/Bptr.

void readme(): readme.c

Contains the readme manual for CALC.

MPR *RECIPROCAL(unsigned long n): i5R.c

Returns 1/n, where 0 < n < R0.

unsigned int REDUCE_NEG(MPI *A, MPI *B, MPI *C): reductio.c

This is Gauss's algorithm for reducing a positive definite binary quadratic form. See L.E. Dickson, Introduction to the theory of numbers, page 69.
The reduced form (A,B,C) satisfies -A < B ≤ A, C ≥ A, with B ≥ 0 if C=A.
The number of steps taken in the reduction is returned.

unsigned int REDUCE_POS(MPI *A, MPI *B, MPI *C): reductio.c

Given an indefinite binary quadratic form ax²+bxy+cy², we use the PQa continued fraction algorithm to determine a reduced form and thence a cycle of reduced forms.
The length of the cyle is returned.
Note: d=b²-4ac > 0, d is not a perfect square and we assume d < 10⁶.
(See explanatory note.)

unsigned int REP_DEFINITE(MPI *a, MPI *b, MPI *c, MPI *m, USI print_flag): reductio.c

Given a positive definite binary quadratic form ax²+bxy+cy², we use an algorithm of Gauss to determine if a given positive integer m is expressible as m = ax²+bxy+cy², x and y integers, gcd(x,y) = 1.
Note: Here d = b² - 4ac < 0, a > 0, c > 0.
(See L.E. Dickson, Introduction to the theory of numbers, pages 74-75.)
print_flag = 1 gives the solutions and unimodular transformations, while print_flag = 0 gives only the solutions.

void ROOTEXPANSION(Stack s): roots.c

Here POLYI P = stackPop(s), MPI *M = stackPop(s). This finds the first M partial quotients of the continued fraction expansion of all real roots of the supplied polynomial P using Lagrange's method and methods presented in a paper by Cantor, Galyean and Zimmer.

MPMATI *ROWSUBI(USI p, USI q, MPI *Aptr, MPMATI *Mptr): i6I.c

Updates Mptr: subtracts Aptr x the p-th row of Mptr from the q-th.
0 ≤ p, q < Mprt->R.

MPI *ROWSUMI(MPMATI *Mptr, USI i): i9.c

Returns the sum of the elements in row i of Mptr.
0 ≤ i < Mptr->R.

int RSV(MPI *Aptr, MPI *Bptr): i1.c

Returns 1 if |Aptr| > |Bptr|,
0 if |Aptr| = |Bptr|, -1 if |Aptr| < |Bptr|.

void RSV_PADIC(MPIA A, MPIA B, USI m, USI n): p-adic.c

RSV_PADIC() is an adaption of one in i1.c and returns 1,0,-1 according as A >,=,< B.
It is assumed that A and B are to the same base.

unsigned long RUSSm(USL a, USL b, USL c, USL p): i5m.c

input: unsigned long ints a, b, c, p, with p > 0.
output: a + bc (mod p).
Russian Peasant multiplication algorithm. Uses the identities
RUSSm(a, b, 2c, p) = RUSSm(a, 2b, c, p),
RUSSm(a, b, c + 1, p) = RUSSm(a + b, b, c, p).
If a, b, c and p are less than 2³², so is RUSSm(a, b, c, p).
From H. Lüneburg, On the Rational Normal Form of Endomorphisms,
B.I. WissenSchaftsverlag, Mannheim/Wien/Zurich, 1987, pp 18-19.
Lüneburg's restriction to 2p<2³² removed by me on 18/4/94.

void SCHNORRGCD(MPI *N): nfunc.c

Applies LLL to [I_m|ND] with N large
to get small multipliers for the extended gcd problem.
See [Matthews].)

void SERRET(MPI *P, MPI **Xptr, MPI **Yptr): nfunc.c

This program finds positive integers X, Y such that
X²+Y²=P, where P=4n=1 is a prime.
The algorithm goes back to Serret and is from the book
Computational methods in number theory, part 1,
edited by H.W. Lenstra and R. Tijdeman.

MPI *SIGMA(MPI *N): primes1.c

Returns sigma(N), the sum of the divisors of N,
Returns NULL if factorization unsuccessful.

MPR *SLVECTOR(MPMATR *A, MPR *C, MPR **VALUE): i6R.c

Input: A matrix of integers A with LI LLL reduced rows spanning a lattice L. C = length-squared of a small lattice vector. Output: if 0 is returned, this means that VALUE is the shortest length. Otherwise a shorter length is returned and VALUE will be NULL.
Used in nfunc.c, in SLVECTORX(), starting with a LLL-reduced matrix and C=||A₁||², eventually 0 is returned. Then FINCKE-POHST is applied to get all the shortest vectors in L with highest nonzero coord > 0 are printed.
(See "Improved methods for calculating vectors of short length in a lattice, including a complexity analysis, U. Fincke and M. Pohst, Mathematics of Computation, 44, 1985, 463-471.)

MPI **SMITHI(MPMATI *Mptr, MPMATI **Pptr, MPMATI **Qptr, USI *ptr, MPI *Eptr): i9.c

Returns the invariant factors of Mptr.
Pptr and Qptr are invertible matrices such that Pptr·Mptr·Qptr
is the Smith normal form Nptr. ptr is the number of invariant factors.
See Rings, Modules and Linear Algebra, B. Hartley and T.O. Hawkes,
Chapman and Hall, 1970. We use a pivoting strategy suggested by George Havas. Eptr is the cutoff above which we bring in MLLL.

MPI **SMITHI1(MPMATI *Mptr, USI *ptr, MPI *Eptr): i9.c

Same as SMITHI, but with no transforming matrices.

void SPRINTI(char *buffer, MPI *Mptr): i5I.c

The decimal digits of the MPI Mptr are placed in the string buffer.
No new-line is incorporated.

void SPRINTR(char *buffer, MPR *Aptr): i5R.c

Prints the MPR Aptr as (Aptr->N)/(Aptr->D).

MPI *SQROOT1(MPI *A, MPI *P, USL n): primes1.c

This returns a solution of x² ≡ A (mod Pⁿ), where P is an odd prime not dividing A. Returns -1 otherwise.
Let d=gcd(a,pⁿ).
Case 1: d=1. Use the standard recursive approach - two solutions if soluble.
                If P=2, care is needed, as in the case of solubility, (i) there is 1 solution if n=1, (ii) 2 solutions if n=2 and (iii) 4 solutions if n ≡ 3.
Case 2: d=Pⁿ. Then x=0 is the solution.
Case 3: d=P^r, 1 < r < n. Write a=P^rA, where P does not divide A.

1. If r is odd, there is no solution.
2. If r is even, say r=2R. Put x=P^RX.
   Then X² ≡ A (mod P^n-2R), which reduces to Case 1.

MPI *SQROOT2(MPI *A, USL n): primes1.c

This returns a solution of x² ≡ A (mod 2ⁿ), A odd. Returns -1 otherwise. Also returns a global variable sqroot2_number=1,2,4 if n=1,2,or n > 2. This variable is used in SQROOT

MPI *SQROOT3(MPI *A, MPI *P, USL n, MPI**EXPONENT): primes1.c

This returns a solution of x² ≡ A (mod Pⁿ), where P is an odd prime possibly dividing A. Returns -1 otherwise. Also returns a "reduced moduli" explained as follows:
If P does not divide A, the story is well-known.
If P divides A, there are two cases:
(i) Pⁿ divides A,
(ii) Pⁿ does not divide A.
In case (i) there are two cases:
(a) n=2m+1, (b) n=2m.
In case (a), the solution is x ≡ 0 (mod P^(m+1)).
In case (b), the solution is x ≡ 0 (mod P^m).
(These are called reduced moduli and are returned as EXPONENT. This variable is used in SQROOT.)
In case (i) gcd(A,Pⁿ)=P^r, r < n. If r is odd, no solution.
If r=2m, write x=(P^m)*X, A=(P^2m)*A1, P not dividing A1.
Then x² ≡ A (mod Pⁿ) becomes X² ≡ A1 (mod P^n-2m).
If P is odd, this has 2 solutions X mod P^n-2m and we get two solutions x (mod P^n-m). If P=2, we get 1 solution mod (2^n-m) if n-2m=1, 2 solutions mod (2^n-m) if n-2m=2, 4 solutions mod (2^n-m) if n-2m > 2.

MPI *SQROOT(MPI *A, MPI *N, MPIA *SOL, MPI **MODULUS, USI *lptr): primes1.c

This finds the solutions of x²≡A (mod N) as residue classes ±SOL[0],...,±SOL[lptr-1] (mod MODULUS), where 0 ≤ SOL[i] < MODULUS. The number of solutions mod N is returned. If there is no solution, -1 is returned, SOL[0]=NULL and lptr=0.

MPI *SQRTM(MPI *x, MPI *p): qres.c

Calculates sqrt(x) (mod p) using A simple and fast probabilistic
algorithm for computing square roots modulo a prime number,
I.E.E.E. Trans. Inform. Theory, IT-32, 1986, 846-847, R. Peralta.
Here x is a quadratic residue mod p. x can be negative.

unsigned long SQRTm(USL x, USL p): qres.c

Returns sqrt(x) (mod p), as above. Here 1 ≤ x < p.
x is a quadratic residue mod p.

Stack STURM(POLYI P): roots.c

Returns a stack of intervals about each of the real roots of P. Each interval contains only one root. If there are no roots, it returns an empty stack. P is supposed to have no rational roots, but is not necessarily squarefree.

void SUB_PADIC(MPIA A, MPIA B, MPI *P, MPIA *DIFF, USI m, USI n, USI *l): p-adic.c

SUB0_PADIC() is an adaption of SUB0_I() in i1.c.
Here A ≥ B and returns l and the array DIFF[]=A-B=DIFF[0]+DIFF[1]P+...+DIFF[l]P^l.

MPI *SUB0I(MPI *Aptr, MPI *Bptr): i1.c

Returns Aptr-Bptr, where Aptr ≥ Bptr ≥ 0.

MPI *SUB0_I(MPI *Aptr, unsigned long b): i1.c

Returns Aptr-b, where Aptr ≥ b ≥ 0.

MPI *SUBI(MPI *Aptr, MPI *Bptr): i1.c

Returns Aptr-Bptr.

MPR *SUBR(MPR *Aptr, MPR *Bptr): i5R.c

Returns Aptr-Bptr.

MPI *SUBM(MPI *Aptr, MPI *Bptr, MPI *Mptr): i5m.c

returns Aptr - Bptr (mod Mptr).
Here 0 ≤ Aptr, Bptr < Mptr.

unsigned long SUBm(USL a, USL b, USL m): i5m.c

Returns a - b (mod m) if m > 0; here 0 ≤ a, b < m < 2³².

MPI *SUBRESULTANT(POLYI P, POLYI Q): pI.c

This returns the resultant of P and Q, using the subresultant
algorithm of p. 130. E. Kaltofen, G. E. Collins etc, Algorithm 4.5.
similar to Knuth, Algorithm C, p. 410.

unsigned int SURD(MPI *D, MPI *T, MPI *U, MPI *V): nfunc.c

This function uses the continued fraction algorithm expansion
in K. Rosen, Elementary Number theory and its applications,
p.379-381 and Knuth's The art of computer programming,
Vol.2, p. 359. It locates the first complete quotient that is reduced
and then uses the function REDUCED(D,U,V,i) above to locate and return
the period of the continued fraction expansion of (U+T*sqrt(D))/V.

MPMATI *SWAP_COLSI(USI p, USI q, MPMATI *Mptr): i6I.c

Interchanges cols p and q (C notation) of Mptr.

MPMATI *SWAP_COLSI1(USI p, USI q, MPMATI *Mptr): i6I.c

Interchanges cols p and q (C notation) of Mptr.
Updates Mptr.

MPMATI *SWAP_ROWSSI(USI p, USI q, MPMATI *Mptr): i6I.c

Interchanges rows p and q (C notation) of Mptr.

MPMATI *SWAP_ROWSSI1(USI p, USI q, MPMATI *Mptr): i6I.c

Interchanges rows p and q (C notation) of Mptr.

void SelOpt( ): menu.c

This function simply prints the "SELECT OPTION: " prompt.

USL TABLENEG(MPI *M, MPI *N): reductio.c

Here 1 ≤ m ≤ n < 10⁶. Calculates h(-d) for all squarefree d with m ≤ d ≤ n. The number h of squarefree d in the range is returned. The output is also sent to tableneg.out.

USL TABLEPOS(MPI *M, MPI *N): reductio.c

Here 2 ≤ m ≤ n < 10⁶. Calculates h(d) for all squarefree d with m ≤ d ≤ n. The number h of squarefree d in the range is returned. The output is also sent to tablepos.out.

MPI *TANGENT(USL n): tangent.c

This constructs the tangent function t(n). See slides by Richard Brent.

MPI *TAU_COMPOSITE(USI n): primes1.c

Returns the value of Ramanujan's tau function by computing its value at prime power factors of n. See BCMATH program.

MPI *TAU_PRIMEPOWER(USI n, USI p): primes1.c

Computes the value of tau(pⁿ), p a prime.

MPI *TAU(USI n)

Returns the value of Ramanujan's tau function without using the prime power factorization of n. It is used in TAU_PRIMEPOWER.

void TESTLOG(MPI *A, MPI *B, MPI *D, MPI *M, MPI *N): log.c

Runs TESTLOG1(A,B,D,R) for R=M,...,N.
This gives a good idea of the true partial quotients of log(a)/log(b).

void TESTLOG1(MPI *A, MPI *B, MPI *D, MPI *R): log.c

This is similar to LOG, but is for use in TESTLOG2.

MPMATI *TRANSPOSEI(MPMATI *Mptr): i6I.c

Returns the transpose of Mptr.

MPI *TWOI( ): i5I.c

Returns 2.

void TryAgain( ): menu.c

Prints "Try again"

void TWOADICSQRT(MPI *A, USI n, MPIA *DIGITS): p-adic.c

TWOADICSQRT() n > 0, returns the first n binary digits of a 2-adic sqroot x of a positive integer a=8k+1. Here x=1 (mod 4). See lectures and solutions.

USL UNIMODULAR(MPI *P, MPI *Q, MPI *R, MPI *S): davison.c

This program expresses a unimodular matrix A=[p,q;r,s] !=I₂ or U=[0,1;1,0] with non-negative coefficients, as a product of the type P, UP, PU, or UPU, where P is a product of matrices of the form U_a=[a,1;1,0], a>0.
The representation is unique.
(See Kjell Kolden, Continued fractions and linear substitutions, Arch. Math. Naturvid. 50 (1949), 141-196.
Also see the corresponding BCMATH program.)

MPI *ZEROI( ): i5I.c

Returns 0.

MPR *ZEROR( ): i5R.c

Returns 0.

MPMATI *ZEROMNI(USI m, USI n): i6I.c

Returns the zero max n matrix.

MPMATR *ZEROMNR(USI m, USI n): i6R.c

Returns the zero max n matrix.

void init( ): init.c

Install built-in function names in table.

void initv( ): init.c

Install built-in void function names in table.

Last modified 14th October 2008