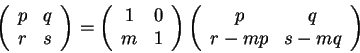Factorising a 2x2 non-singular non-negative matrix

Input: a non-singular matrix A = [p,q;r,s]

, p, q, r, s ≥ 0.
A non-negative matrix B = [a,b;c,d]

is called row-balanced if (a < c & b > d) or (c < a & d > b).
With L = [1,0;1,1]

and R =

, we express A uniquely as a product of positive powers of L and R, followed by a row-balanced B.
We exclude A = I<sub>2</sub>

and A =

.
With U_a = [a,1;1,0]

, we note that U_a₀··· U_{a_2n} = R^a₀L^a₁··· R^a_2nU₀ and that U_a₀··· U_{a_2n+1} = R^a₀L^a₁··· L^a_2n+1I₂.

The number of terms L and R in the factorisation is returned.

We remark that if A is a positive unimodular matrix, the factorisation cannot consist wholly of powers of R or powers of L.

If r ≥ p and s ≥ q, we take m = min([r/p], [s/q]) if p > 0 and q > 0, m = [r/p] if q = 0 and m = [s/q] if p = 0 and use the identity

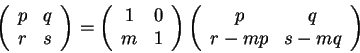= L^mB.

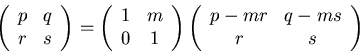whereas if p ≥ r and q ≥ s, we take m = min([p/r], [q/s]), if r > 0 and s > 0, m = [p/r] if s = 0 and m = [q/s] if r = 0 and use the identity

= R^mB.

B is a non-negative matrix whose entries are not greater than before and for which at least one entry has strictly decreased.

(See On continued fractions and finite automata, George N. Raney, Math. Annalen, 206, 265-283 (1973).)

Last modified 5th February 2009
Return to main page