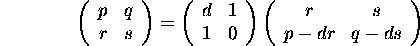
![[p,q;r,s]](../gifs/pqrs.gif) ≠
≠ 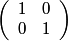 or U0 =
or U0 = ![[0,1;1,0]](../gifs/0110.gif) , with non-negative coefficients, as a product of the type
P, U0P, PU0, or U0PU0, where P is a product of matrices of the form Uc =
, with non-negative coefficients, as a product of the type
P, U0P, PU0, or U0PU0, where P is a product of matrices of the form Uc = ![[c,1;1,0]](../gifs/c110.gif) , c > 0.
, c > 0.While r > 0 and s > 0, we repeatedly use the identity
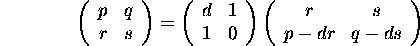
where d = min([p/r],[q/s]).
The process eventually stops, either because r = 0, in which case we reach UqU0,
or because s=0, in which case we reach Up.
This is a BCMATH translation of a BC program.
Last modified 24th June 2010
Return to main page