Finding the chromatic and flow polynomials of a linear matroid over ℤp

Let C=[C1|⋯|Cn] be an m × n matrix with non-zero columns over ℤp. Then the chromatic polynomial of C is defined by

PC(λ) = ΣA(-1)|A|λrank(C)−rank(A),

where A runs over the column submatrices of C, including the empty set. This is the chromatic polynomial of the matroid MC formed by the columns of C under the normal rank function. See Characteristic polynomials with integer roots, a talk by Gordon Royle, 2012 and Matroid theory, D.J.A. Welsh, p. 262. For background information about matroids, see What is a Matroid?, James Oxley.

PC(λ) has the form

PC(λ) = λr − ar −1λr −1 + ⋯ + (−1)ra0,

where r = rank(C) and the ai ≥ 0. It is conjectured that these coefficients form a logarithmic concave sequence, i.e., ai2 ≥ ai−1ai+1 and hence unimodal.

The flow polynomial of C is defined by

FC(λ) = ΣA(-1)n−|A|λ|A| − rank (A).

FC(λ) has the form

FC(λ) = λs − bs −1λs −1 + ⋯ + (−1)sb0,

where s = nullity(C) and the bj ≥ 0. In fact FC(λ) is the chromatic polynomial of the dual matroid M*C. More explicitly, FC(λ) = PD(λ), where D = [D1|⋯|Ds] is a matrix whose columns form a basis for the null space of C, i.e. CD⊥ = 0. Also see The Tutte Polynomial, Henry H. Crapo, Aequationes mathematicae, 211-229, Theorem III, p. 227, for a combinatorial interpretation in terms of counting H-cycles with kernel 0, in the case where MC is a regular matroid.

These polynomials generalize two well-known polynomials associated with a graph:

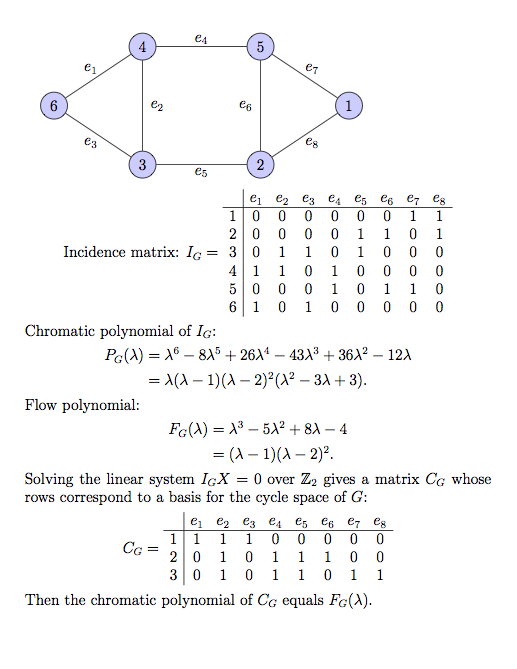
Example 1

Example 2. The complete bipartite graph K3,3:

PG(λ) = λ6− 9λ5+ 36λ4− 75λ3+ 78λ2− 31λ = λ(λ − 1)(λ4− 8λ3 + 28λ2− 47λ + 31).
FG(λ) = λ4 − 9λ3 + 30λ2 − 42λ + 20 = (λ − 1 )(λ − 2)(λ2 − 6λ + 10).

Example 3. The Petersen Graph:

PG(λ) = λ10 − 15λ9+ 105λ8 − 455λ7+ 1353λ6 − 2861λ5+ 4275λ4 − 4305λ3+ 2606λ2 − 704λ = λ(λ − 1)(λ − 2)(λ7 − 12λ6 + 67λ5 − 230λ4 + 529λ3 − 814λ2 + 775λ − 352.
FG(λ) = λ6 − 15λ5+ 95λ4 − 325λ3+ 624λ2 − 620λ+ 240 = (λ − 1)(λ − 2)(λ − 3)(λ − 4)(λ2 − 5λ + 10).

Example 4. The cubical graph:

PG(λ) = λ8 − 12λ7+ 66λ6 − 214λ5+ 441λ4 − 572λ3+ 423λ2 − 133λ = λ(λ − 1)(λ6 − 11λ5 + 55λ4 − 159λ3 + 282λ2 − 290λ + 133).
FG(λ) = λ5 − 12λ4 + 58λ3 − 137λ2 + 154λ − 64 = (λ − 1)(λ − 2)(λ3 − 9λ2 + 29λ − 32).

(see link for the 2 and 3-colourings).

The algorithm used here is only appropriate for small graphs. For faster and more sophisticated algorithms, the reader should consult references 1 and 6 below.

References

  1. Martin H.G. Anthony, Computing chromatic polynomials, Ars Combinatoria 29C (1990) 216-220.
  2. Tamás Hubai, The chromatic polynomial.
  3. B. Jackson, Zeros of chromatic and flow polynomials of graphs, J. Geom., 76, 95-109 (2003).
  4. K.R. Matthews, An example from power residues of the critical problem of Crapo and Rota, J. Number Theory 9 (1977) 203-208.
  5. James Oxley, The contributions of Dominic Welsh to matroid theory.
  6. Code for Computing Tutte Polynomials, David Pearce.
  7. Ronald C. Read, An Introduction to Chromatic Polynomials, J. Combinatorial Theory 4 (1968) 52-71.
  8. Richard Stanley, Log-Concave and Unimodal Sequences in Algebra, Combinatorics and Geometry.
  9. W.G. Tutte, Graph Theory, CUP 1984.
  10. Vince Vatter, Binomial coefficients, unimodality, log-concavity.
  11. Eric W. Weisstein,Chromatic Polynomial, MathWorld - A Wolfram Web Resource.
This program calculates PC(λ) and FC(λ).
Enter the matrix of integers from 0,1,...,p−1, (with nonzero columns) either
(i) as a string of mn integers separated by spaces,
or
(ii) cut and pasted from a text or other file, with entries separated by spaces and each row ended by a newline. See creating the incidence matrix of a graph.

row dimension (2 ≤ m ≤ 15):
column dimension (1 ≤ n ≤ 15):
prime:
Matrix:

Last modified 16th September 2013
Return to main page