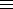Solving the diophantine equation x2 – Dy2 = N, D > 0 and not a perfect square, N ≠ 0

This first finds all primitive fundamental solutions, then all fundamental solutions for the diophantine equation x2 – Dy2 = N, D > 0, D not a perfect square, N ≠ 0. We have to find all primitive fundamental solutions of the equations x2 – Dy2 = N/f2 for all divisors f of N such that f2 divides N; these belong to classes P, where P2 D (mod |N| ).
E = 1 is verbose and prints partial and complete quotients, as well as convergents, up to the end of a period (or double period, in the case of odd period).

Our algorithm (LMM) goes back to Lagrange 1770 and should be better known, as it generalises the well-known continued fraction algorithm for solving Pell's equation. (See a slide-talk (pdf) by Keith Matthews.)

Another approach to the algorithm, using ideals, was discovered by Richard Mollin - see Expositiones Math. 19 (2001) 55-73.

The standard method is due to Gauss - see G.B. Mathews Number Theory, page 97 or John Robertson, Computing in quadratic orders, page 14.

The book L'équation diophantienne du second degré, Alain Faisant, Hermann 1991, has an algorithm for getting all solutions, which also uses continued fractions.

Enter D (< 1020):
Enter N (≠ 0):
Enter E (0 or 1):

Last modified 7th March 2015
Return to main page