Some examples of generalized 3x+1 mappings of Benoit Cloitre

Mapping T₁

The iterates y, T₁(y), T₁(T₁(y)),... of the function

are printed and the number of steps taken to reach one of the integers 0, -1, -4, -19 is recorded.

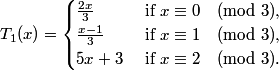
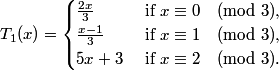
Benoit Cloitre in an email to Jeff Lagarias dated July 19, 2011, has conjectured that every trajectory starting from a positive integer will eventually reach 0.
It is also clear experimentally that any trajectory starting from a negative integer will eventually reach one of three cycles beginning with -1, -4 or -19.

Cycles: (i) 0,0; (ii) -1,-2,-1; (iii) -4,-17,-6,-4; (iv) -19,-92,-31,-152,-51,-34,-167,-56,-19.

Heuristics: Visit Generalized 3x+1 functions and Markov matrices, where we find, with d = 3 and m₀ = 2, m₁ = 1, m₂ = 15 and x₀ = 0, x₁ = 0, x₂ = 3,
\[ Q(3)=\left[ \begin{array}{ccc} 1/3 & 1/3 & 1/3\\ 1/3 & 1/3 & 1/3\\ 0& 1 & 0 \end{array} \right]. \] has stationary vector (1/4, 1/2, 1/4). Also

(2/3)^1/4(1/3)^1/2(15/3)^1/4 < 1.

Consequently we expect all trajectories to eventually cycle.

Mapping T₂

Benoit Cloitre in an email to Jeff Lagarias dated July 20, 2011, has conjectured that every trajectory starting from a positive integer will eventually reach 0 or 2.
It is also clear experimentally that any trajectory starting from a negative integer will eventually reach -1.

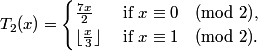Cycles: (i) 0,0; (ii) 2,7,2: (iii) -1,-1.

Heuristics: This function can be regarded as a six-branched mapping. Accordingly, visit Generalized 3x+1 functions and Markov matrices, where we find,
with d = 6 and m₀ = 21, m₁ = 2, m₂ = 21, m₃ = 2, m₄ = 21, m₅ = 2 and x₀ = 0 = x₁ = x₂ = x₃ = x₄ = x₅, that
\[ Q(6)=\left[ \begin{array}{cccccc} 1/2 & 0 & 0 & 1/2 & 0 & 0\\ 1/3 & 0 & 1/3& 0 &1/3 & 0\\ 0 &1/2 & 0 & 0 &1/2 & 0\\ 0 &1/3 & 0 & 1/3 & 0 & 1/3\\ 0 & 0 &1/2 & 0 & 0 & 1/2\\ 0 &1/3 & 0 & 1/3 & 0 & 1/3 \end{array} \right]. \] This Markov matrix has stationary vector (2/15,3/15,2/15,3/15,2/15,3/15) and the weighted product (21/6)^2/15(2/6)^3/15 ··· is less than 1, and this allows us to predict that all trajectories will eventually cycle.

Mapping T₃

For this mapping, Benoit Cloitre has conjectured that every trajectory starting from a positive integer will eventually reach 0, 4, 6 or 24.
It is also clear experimentally that any trajectory starting from a negative integer will eventually reach -1.

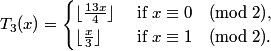Cycles: (i) 0,0; (ii) 4,13,4: (iii) 6,19,6 (iv) 24, 78,...,73,24 (length 87) (v) -1,-1.

Heuristics: This function can be regarded as a twelve-branched mapping and an analysis of the 12x12 Markov matrix Q(12) suggests that all trajectories will eventually cycle.

Mapping F_m

First f_m(x) is defined by

Then

For m = 3, 5 and m ≥ 7, Benoit Cloitre conjectures that the trajectories of F_m will eventually enter one of finitely many cycles.
This mapping can be regarded as a 2m-branched generalized 3x+1 mapping if m is even, and an m-branched mapping if m is odd. See the BC program cloitrem in which function(m) prints F_m(x) in two ways. For example,

Here all trajectories appear to enter one of six cycles (i) 0,0 (ii) -1,-1 (iii) 1,2,1 (iv) -2,-3,-4,-2 (v) -5,-10,-7 (vi) 19,38,25,50,33,22,44,29,19.

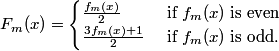
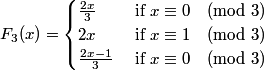
We can use the Markov matrix approach of generalized 3x+1 functions to predict the behaviour of trajectories. See manuscript.

We find for example, with m = 3, m₀ = 2, m₁ = 6, m₂ = 2 and x₀ = 0 = x₁ = x₂,
\[ Q(3)=\left[ \begin{array}{ccc} 1/3 & 1/3 & 1/3\\ 0 & 0 & 1\\ 1/3 & 1/3 & 1/3 \end{array} \right], \] which has stationary vector (1/4, 1/4, 1/2). Also

(2/3)^1/4(6/3)^1/4(2/3)^1/2 < 1.

Consequently we expect all trajectories to eventually cycle.

A list of cycles found for 2 ≤ m ≤ 2000 is also attached.
The examples of F₂₉ and F₁₅₃ are striking, as there are apparently 165 and 416 cycles, respectively.

Last modified 8th December 2020
Return to main page