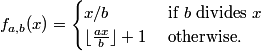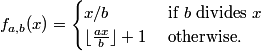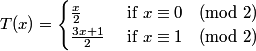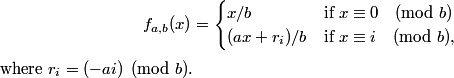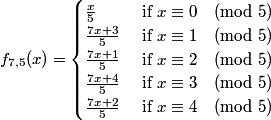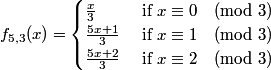A generalization of the 3x+1 mapping due to Geoffrey C. Caveney

In a posting to sci.math on February 1, 1998, Geoffrey Caveney defined a mapping fa,b: ℤ → ℤ as follows: Let a > b > 1, gcd(a,b) = 1. Then

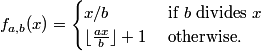
For example, a = 3, b = 2 gives the 3x+1 mapping:

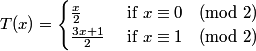
Caveney was not aware that his mapping was a special case of a mapping studied by Herbert Möller in 1978, which in turn was generalized in 1984 to the case of a relatively prime mapping by K.R. Matthews and A.M. Watts. Caveney's mapping can also be written as a b-branched mapping:

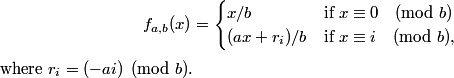
This reduces to W. Carnielli's mapping if a = b+1, as ri = b - i if 1 ≤ i < b.

According to Möller, it seems certain that for x ∈ ℤ, the sequence of iterates x, T(x), T2(x), ... always eventually enters a cycle if a < bb/(b-1) and that regardless of this inequality, there are only finitely many such cycles. Also if a > bb/(b-1), the prediction is that most trajectories will be divergent.

We note that writing a=b+x, x ≥ 1, we have log(1+x/b) < x/b, (1+x/b)b < ex, so if x + b > ex, we have (1+x/b)b < b+x and hence (b+x)b-1 < bb.
Hence a < bb/(b-1) if b > ea-b -(a-b). In particular, we have the following inequalities:

  1. b+1 < bb/(b-1) iff b ≥ 2.
  2. b+2 < bb/(b-1) iff b ≥ 3.
  3. b+3 < bb/(b-1) iff b ≥ 12.
  4. b+4 < bb/(b-1) iff b ≥ 42.
Caveny experimented with a/b: 4/3, 5/3, 5/4, 6/5, 7/5, 8/5 and 7/6. It seems that for f7,5, where

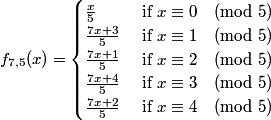
all iterates will eventually enter one of the following cycles:
  1. 0,0
  2. -1,-1
  3. 1,2,3,5,1
  4. -2,-2
  5. 6,9,13,19,27,38,54,76,107,150,30,6
  6. -17,-23,-32,-44,-61,-85,-17
  7. -33,-46,...,-165,-33 (length 58)
It seems that for f5,3, where

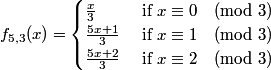
all iterates will eventually enter one of the following cycles:
  1. 0,0
  2. -1,-1
  3. 4,7,12,4
  4. 8,14,24,8.
For f8,5, we have found five cycles:
  1. 0,0
  2. -1,-1
  3. 4,7,1,2,20,4
  4. -11,-17,-27,-43,-68,-108,-172,-275,-55,-11
  5. -49,-78,...,-245,-49 (length 62)
Here a = 8 > bb/(b-1) = 55/4 = 7.476···. It seems certain that the trajectories starting with 8 and -98 diverge.

The viewer can experiment with f5,3 and f7,5:

Enter y:

Mapping f5,3
Mapping f7,5

Last modified 22nd August 2011
Return to main page