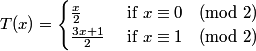
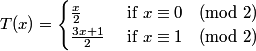
It is conjectured that every trajectory starting from a non-zero integer will end in one of the (non-zero) numbers in this list and subsequently cycle:
1,2,1;
-1,-1;
-5,-7,-10,-5;
-17,-25,-37,-55,-82,-41,-61,-91,-136,-68,-34,-17.
Also see Generalized 3x+1 functions and Markov matrices.
Last modified 2nd February 2006
Return to main page