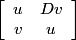Solving Pell's equation without irrational numbers

The algorithm is due to Norman J. Wildberger at J. Integer Sequences, Vol. 13 (2010) 10.4.3. The BCMATH version is based on the BC version.

Here D > 1 is a nonsquare integer. We construct matrices A_k =

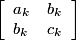with a_k > 0 > c_k with b_k² - a_kc_k = D and unimodular matrices N_k, k ≥ 0.
Starting with A₀ =

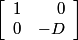and N₀ = I₀, and N_k = M₁ ⋯ M_k if k ≥ 1, where M_i = L =

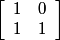or R =

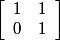and M₁ = R, we choose M_k+1 = R if a_k + 2b_k + c_k < 0, and choose M_k+1 = L if a_k + 2b_k + c_k > 0.

We have N_k^tA₀N_k = A_k for k ≥ 0.

For some n > 0, N_n^tA₀N_n=A₀, where N_n is a positive matrix of the form 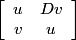and (u,v) is the least positive solution of Pell's equation. In the factorization of N_n, the M_i form a palindromic sequence.

The negative Pell equation will be soluble if and only if there exists a k such that A_k = 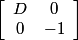, in which case, A_k will be at the centre of symmetry and N_k will have the form 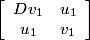. Then (u, v) = (u₁² + Dv₁², 2u₁v₁) and (u₁, v₁) will be the least positive solution of the negative Pell equation.

Note that in Wildberger's paper, on page 7, the equation N = MM^t is not correct and should be replaced by N = MM⁺, where M⁺ = .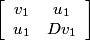

Wildberger does not prove that the solutions found are the least positive solutions, but this can be demonstrated by considering George Raney's L-R factorization algorithm applied to matrices 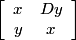and 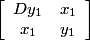, where x² - Dy² = 1 and x₁² - Dy₁² = 1.

E = 0 prints the least positive solution of Pell's equation x² - Dy² = 1 and determines if the negative Pell equation x² - Dy² = -1 is soluble, in which case the least positive solution is found.

Last modified 21st February 2015
Return to main page