Solving ax=b, where x is a p-adic integer and a >1, b > 0 are integers
This algorithm is due to Victor Scharaschkin.
One possible use is for creating good abc triples by virtue of the equation
(ax-b)+b=ax.
Let N=ordpa and aN=1+epg, where p does not divide e.
Then with a suitable definition of ax, the equation ax=b is soluble in the p-adic integers if and only if it is soluble in Z/pg Z, in which case the solution is unique.
In the case of solubility, we find integer p-adic approximations ng, ng+1, ..., ng+k to x.
The ni satisfy for i ≥ g:
- ani
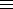 b (mod pi )
b (mod pi )
- ni+1
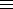 ni (mod pi-g ).
ni (mod pi-g ).
We have to restrict p to be less than 232 – 216=4294901760 for the Shanks baby step/giant step algorithm to work.
Last modified 25th March 2005
Return to main page
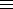 b (mod pi )
b (mod pi )
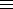 ni (mod pi-g ).
ni (mod pi-g ).
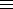 b (mod pi )
b (mod pi )
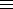 ni (mod pi-g ).
ni (mod pi-g ).