Brian Gurbaxani's mappings

Mapping P₄

In an email dated April 1, 2021, Brian Gurbaxani (briangurbaxani@gmail.com) sent me the following varation of the 3x+1 mapping:

If n is even, T(n) = n/2; if n is odd and divisible by 5, then T(n) = (m*n/5 + 1)/2, otherwise T(n) = (3n + 1)/2, for some fixed odd integer m ≥ 3.

This is very similar to the 3x+1 mapping unless n is odd and divisible by 5, and if we set the parameter m = 15, it is exactly the 3x+1 mapping.
He conjectured that the iterative sequence x, T(x), T(T(x)),... is always bound to converge to one of a finite number of finite cycles for all m ≤ 73 (later changed to m < 73).

Mapping P4 can be regarded as a d-branched generalized 3x+1 mapping T: ℤ → ℤ, where T(x) = int(m_ix/d) + X_i, if x ≡ i (mod d), where d = 10,
m₀ = 5, m₁ = 15, m₂ = 5, m₃ = 15, m₄ = 5, m₅ = m, m₆ = 5, m₇ = 15, m₈ = 5, m₉ = 15 and

X₀ = 0, X₁ = 1, X₂ = 0, X₃ = 1, X₄ = 0, X₅ = 1, X₆ = 0, X₇ = 1, X₈ = 0, X₉ = 1:

\[ T(x)=\left\{ \begin{array}{cc} x/2 & \mbox{ if $x\equiv 0\pmod{10}$}\\ (3x+1)/2 & \mbox{ if $x\equiv 1\pmod{10}$}\\ x/2 & \mbox{ if $x\equiv 2\pmod{10}$}\\ (3x+1)/2 & \mbox{ if $x\equiv 3\pmod{10}$}\\ x/2 & \mbox{ if $x\equiv 4\pmod{10}$}\\ (mx+5)/2 & \mbox{ if $x\equiv 5\pmod{10}$}\\ x/2 & \mbox{ if $x\equiv 6\pmod{10}$}\\ (3x+1)/2 & \mbox{ if $x\equiv 7\pmod{10}$}\\ x/2 & \mbox{ if $x\equiv 8\pmod{10}$}\\ (3x+1)/2 & \mbox{ if $x\equiv 9\pmod{10}$} \end{array} \right. \] This mapping is of type (b) where type (b) means gcd(m_i, d²) = gcd(m_i, d) for 0 ≤ i ≤ d - 1.

Then conjecturally, we get everywhere cycling if and only if the weighted product P = Π_{0 ≤ i ≤ d-1}(m_i/d)^p_i < 1, where (p₀, ..., p_d-1) is the stationary vector of the Markov matrix Q(d), which is defined in that paper.

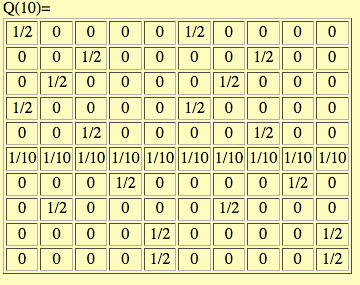
It seems certain that the 10×10 Markov matrix Q(10) is independent of m, but I haven't the patience to prove this.

We calculate Q(10) for m = 73, using the BCMath program Generalized 3x+1 functions and Markov matrices.

This matrix has stationary vector (1/110)(10,14,13,8,10,10,14,13,8,10) and the weighted product P satisfies

P = (1/2)¹⁰ (3/2)¹⁴ (1/2)¹³ (3/2)⁸ (1/2)¹⁰ (m/10)¹⁰ (1/2)¹⁴ (3/2)¹³ (1/2)⁸ (3/2)¹⁰ < 1

if and only if m < 5(2¹¹⁾/3^(9/2) = 72.988...,

So we expect everywhere cycling if and only if m < 73.

The case m = 73 is interesting. We expect to find trajectories n₀, T(n₀), T(T(n₀)),...that appear to be divergent. One such example is n₀ = 100545. David Bařina has followed this trajectory for 20,400,000,000 iterations reaching an iterate of 144,284 digits.

Conjecturally, (T^k(n₀))^1/k → P = 1.0000143...

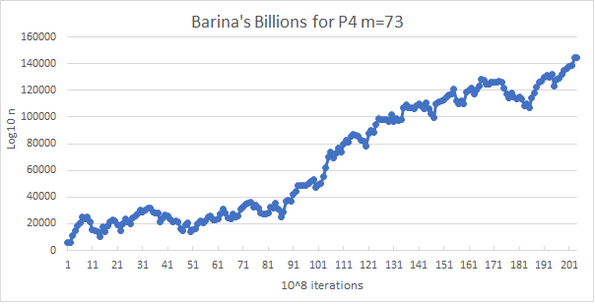(graph supplied by Brian Gurbaxani)

It can take many iterations to reach a cycle. For example,

n₀ = 10⁵⁰⁰⁰ + 1 took 849,740,625 iterations to reach 1,
n₀ = -10⁵⁰⁰ + 1 took 65,501,346 iterations to reach -1,
n₀ = 33145 took 1,400,642,131 iterations to reach 71.

My CALC cycle program finds 18 cycles with starting points (and lengths):

0 (1), -1 (1), 1 (2), 5 (11), -5 (9), -17 (6), 71 (58), -1265 (5470), -1237 (43), -4337 (21), -3257 (21), -4129 (21), 505 (807), -1375 (21), -1055 (21), -1385 (21), -4313 (21), -4157 (1923).

Mapping P₂

Here we are dealing with a 6-branched mapping: \[ T(x)=\left\{ \begin{array}{cc} x/2 & \mbox{ if $x\equiv 0\pmod{6}$}\\ (5x+1)/2 & \mbox{ if $x\equiv 1\pmod{6}$}\\ x/2 & \mbox{ if $x\equiv 2\pmod{6}$}\\ (7x/3+1)/2 & \mbox{ if $x\equiv 3\pmod{6}$}\\ x/2 & \mbox{ if $x\equiv 4\pmod{6}$}\\ (5x+1)/2 & \mbox{ if $x\equiv 5\pmod{6}$}\\ \end{array} \right.. \] In terms of the integer part symbol:

T(x) = int(m_ix/6)+X_i, if x ≡ i (mod 6), i = 0,...,5, and where

m₀ = 3, m₁ = 15, m₂ = 3, m₃ = 7, m₄ = 3, m₅ = 15,

X₀ = 0, X₁ = 1, X₂ = 0, X₃ = 1, X₄ = 0, X₅ = 1.

The Markov matrix approach can be used, as gcd(m_i, d²) = gcd(m_i, d) for all i, with d = 6.

We calculate the Markov matrix Q(6) using the BCMath program Generalized 3x+1 functions and Markov matrices.

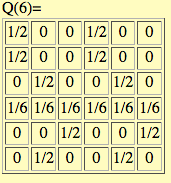
This has stationary vector (6/26, 4/26, 3/26, 6/26, 4/26, 3/26) = (p₀,p₁,p₂,p₃,p₄,p₅) for brevity.

The weighted product is

P = (3/6)^(6/26)(15/6)^(4/26)(3/6)^(3/26)(7/6)^(6/26)(3/6)^(4/26)(15/6)^(3/26)
= 5⁷7⁶/(2²⁶3⁶) = 0.1878... <1.

Hence we expect all trajectories to eventually cycle.

My CALC cycle program finds 13 cycles with starting points (and lengths): 0 (1), -1 (2), 1 (4), -3 (1), 21 (309), 7 (6), -63 (20), -41 (20), 141 (6), 85 (6), 121 (6), 1303 (33), 69721 (44), and I am certain that all trajectories will eventually enter one of these cycles.

Mapping m = 71

Here we are dealing with a 10-branched mapping: \[ T(x)=\left\{ \begin{array}{cc} x/2 & \mbox{ if $x$ is even,}\\ (\frac{71x}{5}+1)/2 & \mbox{ if $x$ is odd and $x\equiv0\pmod{5}$,}\\ (3x+1)/2 & \mbox{ if $x$ is odd and $x\not\equiv0\pmod{5}$.} \end{array} \right. \] In terms of the integer part symbol:

T(x) = int(m_ix/10)+X_i, if x ≡ i (mod 10), i = 0,...,9, and where

m₀ = 5, m₁ = 15, m₂ = 5, m₃ = 15, m₄ = 5, m₅ = 71, m₆ = 5, m₇ = 15, m₈ = 5, m₉ = 15;

X₀ = 0, X₁ = 1, X₂ = 0, X₃ = 1, X₄ = 0, X₅ = 1, X₆ = 0, X₇ = 1, X₈ = 0, X₉ = 1.

We expect all trajectories to eventually cycle.

My CALC cycle program finds 28 cycles with starting points (and lengths): 0 (1), -1 (1), 1 (2), 5 (12), -17 (65), 7 (6), 155 (7), -385 (75), 283 (7), 115 (7), 185 (7), 325 (7), 163 (44), 235 (7), 265 (7), 323 (7), 403 (7), 686195 (412), -915755 (173), 247123 (651), 558763 (997), 252035 (412), 175087 (890), -7523725 (585), 1559551 (412), -1578517 (173), 589015 (412), 900175 (412), 1167131 (412).

I conjecture that all trajectories will eventually enter one of these cycles.

Note that the number of iterations is limited to 100000, so it is possible for some of the listed cycles not to be reached.

For example, the trajectory starting with x = -3546464672 takes 71172 iterations to reach the cycle beginning with -17.

Last modified 15th June 2021
Return to main page