Calculating the backward continued fraction of a quadratic irrational

This program finds the backward continued fraction expansion of a quadratic irrational α = (u + t√d)/v, where d,t,u,v are integers, d >1, and nonsquare, t and v nonzero.
With ξ₀ = α, for i ≥ 0, a_i = int(ζ_i) + 1 and ζ_i+1 = 1/(a_i - ζ_i), we get a finite continued fraction which eventually becomes periodic

where a_i ≥ 2 for i ≥ 1.

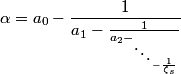
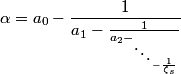
Here a quadratic surd α is reduced if α > 1 > α' > 0 and these are the surds which have a purely periodic continued fraction expansion. See implementation as a BC program.

This continued fraction is mentioned in F. Hirzebruch's paper Hilbert modular surfaces, L'Enseignement Math. 19 (1973) and a paper by Don Zagier, A Kronecker Limit Formula for Real Quadratic fields, Math. Ann, 213, 153-184 (1975) especially pages 177-183. Also see Zetafunktionen und quadratische Körper, Eine Einführung in die höhere Zahlentheorie, Don Zagier, Springer 1981.
Hirzebruch on page 241 proved that if p=4n+3 is a prime and h(p) = 1, then h(-p) = (a₁ + ··· + a_r)/3 - r, where r is the period length of the least integer continued fraction of √p.

Here h(p) is the class number of the real quadratic field ℚ(√p) and h(-p) is the class number of the imaginary quadratic field ℚ(√-p).

Hirzebruch also noted that h(-p) = (-b₁+b2 - ··· + b_2s)/3, where the b_i are partial quotients of the simple continued fraction expansion of √p and 2s is the period length.

The convergents A_i/B_i are calculated as follows:
A_-1 = 1, B_-1 = 0, A₀ = a₀, B₀ = 1,
A_i = a_iA_i-1 - A_i-2, B_i = a_iB_i-1 - B_i-2, i ≥ 1.

We first convert α to (P + √d)/Q, where Q divides d - P² and gcd(P, Q, (d - P²)/Q) = 1.
We print the partial quotients a_n, the convergents A_i/B_i and complete quotients ζ_i with the period partial quotients in bold font.

Last modified 23rd November 2011
Return to main page