Arthur Josef Alwin Wieferich
There are 4 important papers by Wieferich, two in 1908 and two in 1909, when he was 24 and 25 years respectively, at that time a student of the University of Münster:
- Beweis des Satzes, daß sich eine jede ganze Zahl als Summe von höchstens neun positiven Kuben darstellen läßt, Math. Ann. 66 (1908) 95-101.
(every integer is the sum of at most 9 cubes and the number 9 is minimal)
- Über die Darstellung der Zahlen als Summen von Biquadraten, Math. Ann. 66 (1908) 106-108.
(every integer is the sum of at most 38 fourth powers)
- Zur Darstellung der Zahlen als Summen von fünften und siebenten Potenzen positiver ganzer Zahlen, Math. Ann. 67 (1909) 61-75.
(every integer is the sum of at most 59 fifth powers and 3806 seventh powers)
- Zum letzten Fermat'schen Theorem, J. für Math. 136 (1909) 293-302.
(if the first case of Fermat's last theorem holds for exponent p, then p must satisfy the congruence 2p-1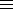 1 (mod p2.) Such a prime is called a Wieferich prime.)
1 (mod p2.) Such a prime is called a Wieferich prime.)
A fifth paper was Zur Driecksgeometrie, J. reine angew. Math.136 (1909) 303-305.
(concerned with elementary projective geometry and Pascal's theorem.)
The following is based on biographical information kindly supplied by Professor Meinhard Peters, Münster from the Universitätsarchiv Münster and the Hauptstaatsarchiv Hannover.
Arthur Wieferich was born on 27th April 1884 in Münster, the son of a businessman. He studied from 1903-1909 in Münster and thereafter became a secondary school teacher in Konitz, Elbing, Zoppot, Neustadt, Jülich, Stade (near Hamburg) and finally Meppen.
From 1945 to 1949 he earned a living as a private tutor.
Athur Wieferich married in 1916 and had no children. He died on the 15th September 1954 in Meppen.
He was a member of the DMV (Deutsche Mathematiker Vereinigung) from 1909 to about 1929.
His five mathematical publications stem from 1908, when he was a student in
Münster. Max Dehn taught a number theory course in 1907 and may have had an influence on Wieferich.
Concerning paper 1, Edmund Landau remarked in the same volume:
I salute the paper of Mr. Wieferich as one of the gratifying recent advances in elementary number theory. The author has solved an old problem conjectured in 1782 and attempted by many number theorists.
A gap in the proof was filled by A.J. Kempner in Math. Ann. 72 (1912) 387-399.
Regarding paper 4, Paulo Ribenboim in his book 13 Lectures on Fermat's Last Theorem (p. 139) remarks:
Then in 1909 came Wieferich. He discovered a criterion for the first case of an entirely different nature. His first proof was an enigma. Few people were able to understand how Wieferich succeeded, like a magician, in unravelling from very complicated formuale, so simple and beautiful a criterion ...
Back to some biographies of past contributors to number theory
Last updated 3rd October 2006
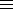 1 (mod p2.) Such a prime is called a Wieferich prime.)
1 (mod p2.) Such a prime is called a Wieferich prime.)