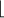Nearest integer Euclidean algorithm

If r is a real number, by [r] we mean the nearest integer to r. Thus |r - [r]| ≤ 1/2 and if r = t + 1/2, where t is an integer, then [r] = t + 1.
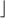Alternatively, [r] = lfloor r + 1/2 rfloor, the integer part of r + 1/2,
Hence [r] = r + θ, where -1/2 < θ &le 1/2.

Then if m and n are integers, n > 0 and q = [m/n], we have m/n = q + θ, where -1/2 < θ ≤ 1/2.
Hence m = nq + nθ, where -n/2 < nθ ≤ n/2.
Hence m = nq + es, where -n/2 < es ≤ n/2 and s is an integer, 0 ≤ s ≤ n/2 and e = 1 if θ ≥ 0, while e = -1 if θ < 0.
We write e = e(m,n).

Then with r0 = m and r1 = n > 0, we define rk recursively for 2 ≤ k ≤ l+1, rk > 0 and ek+1 = e(rk-1,rk), where qk = [rk-1 / rk] for 1 ≤ k ≤ l:

r0=r1q1 + e2r2 (-r1 / 2 < e2 r2 ≤ r1 / 2)
r1=r2q2 + e3r3 (-r2 / 2 < e3 r3 ≤ r 2 /2)
···
rk-1=rkqk + ek+1rk+1 (-rk / 2 < ek+1 rk+1 ≤ rk / 2)
···
rl-1=rlql

Then rl = gcd(m,n).

The sk and tk are also printed in tabular form, where it is convenient to define e0 = 1 = e1 and where

s0 = 1, s1 = 0,eksk = sk-2 – qk-1sk-1,
t0 = 0, t1 = 1, ektk = tk-2 – qk-1tk-1, k = 2,..., l+1.

Then rk = skm + tkn for 0 ≤ k ≤ l+1, where rl+1 = 0. The number of steps is no greater than the number in Euclid's algorithm.

(Based on Exercise 5, page 67, Elementary Number theory and its applications, by Ken Rosen.
Also see Chapter 39 (Kettenbrüche nach nächsten Ganzen), page 168, Kettenbrüche, by Oscar Perron, Chelsea 1950.
We print the nearest integer continued fraction expansion m/n = q1+e2/q2+ ⋯ +el/ql.

Enter m:
Enter n (> 0):
Last modified 26th January 2009
Return to main page