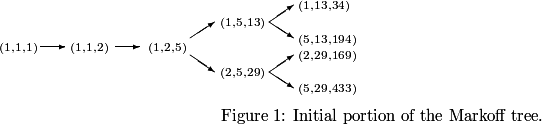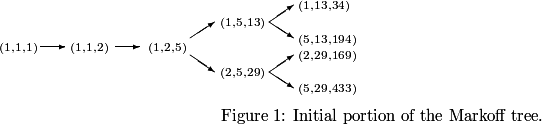Finding all ordered Markoff triples (x,y,z) with 5 ≤ z ≤ upper bound

The positive solutions (x,y,z), x ≤ y ≤ z, of the diophantine equation x2+y2+z2=3xyz form a tree rooted at (1,1,1), using the branching operations

(x,y,z) → (x,z,3xz-y),
(x,y,z) → (y,z,3yz-x).

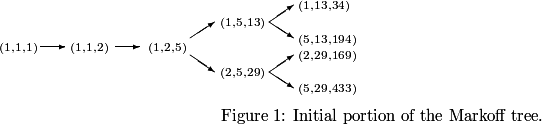
This program finds all ordered Markoff triples (x,y,z), where (a) 5 ≤ z ≤ n or (b) max(x,y) ≤ n and 5 ≤ z.
This is a BCMATH conversion of a modification of a BC program. The recursion was supplied by Alan Offer.

Enter n (≥ 5):

(a) z ≤ n
(b) max(x,y) ≤ n

Last modified 14th November 2013
Return to quadratic diophantine equations page