Generating equivalent quadratic surds

This program takes a unimodular matrix A = [p,q;r,s] (i.e. Δ = ru – st = ±1) and a quadratic surd ξ = (a + √d)/c, where c divides d – a2 and produces η = (rξ + s)/(tξ + u). Then ξ and η will have regular continued fraction expansions which ultimately agree. Similarly for the nearest integer and nearest square continued fraction expansions. If ξ=(a + √d)/c, then η = (A + √d)/C, where A = Δ(brt + a(ru + st) + cus), C = Δ(bt2 + 2atu + cu2) and b = (a2 – d)/c.

  1. C divides d – B2.
  2. If gcd(a,b,c) = 1, then gcd(A,B,C) = 1.
1. follows from the equation A2– d = BC, where B = Δ(br2 + 2ars + cs2).

To prove 2, suppose p is a prime dividing A,B and C. Then

brt + a(ru + st) + cus ≡ 0 (mod p)
br2 + 2ars + cs2 ≡ 0 (mod p)
bt2 + 2atu + cu2≡ 0 (mod p).

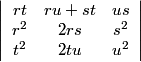This can be regarded as a system of three homogeneous linear equations (mod p) in b,a and c
whose coefficient determinant = -Δ, so p divides a,b and c.

This is a BCMATH translation of a BC program.

Enter p:
Enter q:
Enter r:
Enter s:
Enter d (1 < d < 1015 and not a square):
Enter t (non-zero):
Enter u:
Enter v: (nonzero)

Last modified 29th October 2009
Return to main page