The vector space axioms, examples: ℝn, set of all functions f : S->ℝ, simple deductions from the axioms, subspaces, linear combinations, examples of subspaces: <v1,...,vn> (the subspace spanned by v1,...,vn), R(A), C(A), N(A) (the row, column and null spaces of a matrix A), numerical examples of null spaces, subspace of Fibonacci sequences.
Linear dependence of a list of vectors, connections with AX=0 having a nontrivial solution, linear independence, columns of a square matrix A are linearly independent if and only if A is non-singular, the left-to-right test for independence, the fundamental theorem of linear algebra:
a list of n vectors, each of which is a linear combination of m given vectors, is linearly dependent if n > m,finite-dimensional vector spaces, basis and dimension of a vector space, coordinate vector [v]β of a vector v relative to a basis β.
Example of coordinate vector, columns of an n x n non-singular matrix form a basis for ℝn, change of basis matrix/change of coordinates matrix, example, a non-trivial finite-dimensional vector space has a basis, the left-to-right basis for the column space of a matrix, a basis for the row space, example.
Basis for the null space of a matrix, example, any two bases of a vector space have the same number of elements, dim(V) (the dimension of vector space V), rank(A), nullity(A), rank(A)+nullity(A)=n if A is m x n, a subspace U of a finite-dimensional dimensional vector space V is also finite-dimensional; moreover (i) dim(U) ≤ dim(V), (ii) dim(U)=dim(V) implies U=V, a linearly independent list of n vectors in a vector space V of dimension n is a basis for V, application to finding a formula for the n-th member of a Fibonacci sequence.
Finished discussion on Fibonacci sequences - special case of theFibonacci numbers, generalisation to k-termed linear recurrence relations, extension of a linearly independent family to a basis, the subspace U+V, dim(U+V) ≤ dim(U)+dim(V), dim(U+V)+dim(U ∩ V=dim(U)+dim(V).
Revision example for calculating bases for C(A), R(A), N(A), worked example on the dimension formula, finding a spanning family for U ∩ V, example in ℝ5, the vector space U⊕V, dim(U⊕V)=dim(U)+dim(V).
Linear transformations, example: TA: ℝn->ℝm, rotations and reflections in the x-y plane, more examples of linear mappings: differentiation, the difference operator, kernel and image of a linear transformation T:U->V, (Ker(T) and Im(T)), Ker(T) is a subspace of U, Im(T) is a subspace of V, Im(T)=< T(u1),...,T(un)> if U=<u1,...,un>, Ker(TA)=N(A), Im(TA)=C(A), rank T=dim(Im(T)), nullity T=dim(Ker(T)).
worked example on Ker(T) and Im(T), rank(T)+nullity(T)=dim(U), if T:U->V is a linear transformation, a posh proof of the formula dim(U⊕V)=dim(U)+dim(V), a linear transformation is determined by its action on a basis.
Example on last theorem, the matrix A=
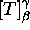 of a linear transformation T, [T(u)]γ=A[u]β, recipes for computing bases for Ker(T) and Im(T) from A, an example.
of a linear transformation T, [T(u)]γ=A[u]β, recipes for computing bases for Ker(T) and Im(T) from A, an example.
L(U,V), the vector space of all linear transformations T: U->V, T1+T2, -T, the zero transformation 0, IV - the identity transformation on V, T2T1 - the composite of two transformations,
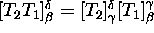 , Tn, f(T),
, Tn, f(T), 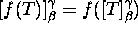 .
.
Injective and surjective linear transformations, T is injective if and only if Ker T={0}, TA is (i) injective iff the columns of A are LI, (ii) surjective iff the rows of A are LI, generalisation of this result to T: U->V, isomorphism, theorems on isomorphisms, applications to matrices, T-1 - the inverse of an isomorphism.
T-1: V->U, is an isomorphism if T: U->V is an isomorphism, (TA)-1=TA-1, connections between isomorphisms and non-singular matrices, some examples, dim U=dim V implies T: U->V is an isomorphism if (i) T is injective or (ii) T is surjective, example.
Change of basis theorem for the matrix of a linear transformation, application to finding all matrices such that A2=A, similarity of matrices, similarity is an equivalence relation, diagonable matrices, application to finding An and hence solving recurrence relations Xm+1=AXm.
Solving dX/dt=AX when A is diagonable, review of determinants, evaluating determinants via row echelon form, cofactor expansion of a determinant, adj A - the adjoint of A, A*(adj A)=det(A)In=(adj A)*A, A-1=(adj A)/det(A), AX=0 has a non-trivial solution iff det(A)=0.
The van der Monde determinant, det (T), where T: V->V is a linear transformation, eigenvalues and eigenvectors, A (n x n) is diagonable over ℝ iff ℝn has a basis of n eigenvectors of A, t is an eigenvalue of A iff det(tIn-A)=0, chA(x)=det(xIn-A) (the characteristic polynomial of A).
Cayley-Hamilton theorem, EA(t)=N(tIn-A) - the eigenspace of A corresponding to the eigenvalue t, gA(t)=dim(EA(t)) (the geometric multiplicity of t), aA(t) - the algebraic multiplicity of t, gA(t) ≤ aA(t), eigenvectors corresponding to distinct eigenvectors are linearly independent, if A is n x n and has n distinct eigenvalues, then A is diagonable, a necessary and sufficient condition for A to be diagonable is (i) chA(x) splits completely and (ii) the geometric and algebraic multiplicities of all eigenvalues are equal, Jn(c) is not diagonable, 3 x 3 example.
Decomposition into principal idempotents using the Lagrange interpolation polynomials, these form a basis for Pn[ℝ], calculating f(A) from the idempotent decomposition of A, direct sum of matrices, GA(t) - the generalised eigenspace of A corresponding to the eigenvalue t.
GA(t) is a subspace of ℝn, GA(t)=N((A-tIn)aA(t)), dim (GA(t))=aA(t), generalised eigenspaces corresponding to distinct eigenvalues of A are independent, the block upper triangular form algorithm, 4 x 4 example, finding An using the block upper triangular form of A.
Computing An for the 4 x 4 example, An-> 0 if all eigenvalues t of A satisfy |t| < 1, calculating (In-A)-1 if all eigenvalues have absolute value less than 1, 3 x 3 example of finding a block upper triangular form, a necessary condition for two matrices to be similar, the integers bA(t).
Classification of Jordan forms of 3 x 3 matrices, definition of the Jordan form JA of A, finding a non-singular matrix P such that P-1AP=JA and 4 x 4 example, 6 x 6 example of finding JA only.
Real inner product spaces, examples - including the Euclidean inner product, ||v|| - the length of v, properties of vector length, Cauchy-Schwarz inequality, the triangle inequality, angle between two vectors.
Orthogonal vectors, non-zero mutually orthogonal vectors are linearly independent, orthonormal family of vectors, orthogonal matrix, A is orthogonal iff the columns of A form an orthonormal family, the general 2 x 2 orthogonal matrix, the Gram matrix of a family of vectors, the Gram matrix of a family of vectors is non-singular iff the family is linearly independent, clarification: more on finding the transforming matrix P for the Jordan form.
Projection of a vector onto a subspace, application to least squares solution of AX=B, the Gram-Schmidt orthogonalisation process, finite-dimensional inner product spaces have orthonormal bases.
Example of the Gram-Schmidt process, extension of an orthonormal family to an orthonormal basis, Parseval's and Bessel's inequalities, real symmetric matrices and quadratic forms, the eigenvalues of a real symmetric matrix are real, a real symmetric matrix is diagonable, eigenvectors corresponding to distinct eigenvalues of a real symmetric matrix are mutually orthogonal, a real symmetric matrix is orthogonally diagonable, application to sketching second degree equations such as 2x2+2xy+2y2=1.
3 x 3 real symmetric matrix example and sketching XtAX=c, positive definite matrices, A is positive definite if A=PtP, where P is non-singular, A is positive definite iff all the eigenvalues of A are positive, A is positive definite implies A=PtP, where P is non-singular, LDU decomposition of a matrix, determinantal criterion for positive definiteness.